题目内容
【题目】在平面直角坐标系
中，已知圆
经过椭圆
的焦点.
（1）求椭圆
的标准方程；
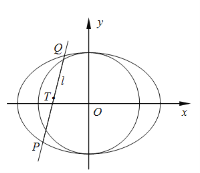
（2）设直线
交椭圆于
两点，
为弦
的中点，
，记直线
的斜率分别为
，当
时，求
的值.
【答案】（Ⅰ）
（Ⅱ）
【解析】
试题分析：（Ⅰ）先确定交点位置：在
轴上，再根据圆与轴交点得等量关系：
；又
,所以
（Ⅱ）设
，表示
，然后根据直线与椭圆方程联立方程组，结合韦达定理表示中点
坐标，并利用条件
化简：
，
，最后代入并利用条件化简得
试题解析：解：（1）因
，所以椭圆
的焦点在轴上，
又圆
经过椭圆的焦点，所以椭圆的半焦距， ……………3分
所以
，即，所以椭圆的方程为. ……………6分
（2）方法一：设
，
，，
联立
，消去
，得
，
所以
，又
，所以
，
所以，， ……………10分
则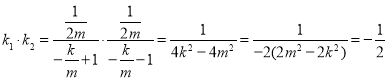
. …………14分
方法二：设，
，， 则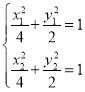
，
两式作差，得
，
又
，
，∴
，∴
，
又，在直线
上，∴
，∴
，①
又在直线上，∴
，②
由①②可得
，
. ……………10分
以下同方法一.
练习册系列答案
寒假学与练系列答案
相关题目
