题目内容
【题目】正方体ABCD﹣A1B1C1D1中,E、F分别是AA1、AB的中点,则EF与对角面A1C1CA所成角的度数是( )
A.30°
B.45°
C.60°
D.150°
【答案】A
【解析】解:∵E、F分别是AA1、AB的中点,
∴EF∥A1B,
则EF与对角面A1C1CA所成角等于A1B对角面A1C1CA所成角
连接BD交AC于O
由正方体的几何特征可得BD⊥平面A1C1CA
即∠BA1O即为EF与对角面A1C1CA所成角
在Rt△BA1O中,∵BA1=2BO
∴∠BA1O=30°
故选A
【考点精析】根据题目的已知条件,利用空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则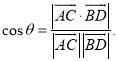 .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
