题目内容
【题目】已知F1、F2分别是双曲线 
﹣ 
=1（a＞0，b＞0）的左、右焦点，以坐标原点O为圆心，OF1为半径的圆与双曲线在第一象限的交点为P，则当△PF1F2的面积等于a2时，双曲线的离心率为（ ）
A.
B.
C.
D.2
【答案】A
【解析】解：设F1F2=2c，由题意知△F1F2P是直角三角形，
∴F1P2+F2P2=F1F22 ，
又根据曲线的定义得：
F1P﹣F2P=2a，
平方得：F1P2+F2P2﹣2F1P×F2P=4a2
从而得出F1F22﹣2F1P×F2P=4a2
∴F1P×F2P=2（c2﹣a2）
又当△PF1F2的面积等于a2
即 
F1P×F2P=a2
2（c2﹣a2）=a2∴c= 
a，
∴双曲线的离心率e= 
= ．
故选A．
练习册系列答案
相关题目
【题目】某工科院校对
， 
两个专业的男女生人数进行调查，得到如下的列联表：
专业 | 专业 | 总计 | |
女生 | 12 | 4 | 16 |
男生 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
（Ⅰ）从
专业的女生中随机抽取2名女生参加某项活动，其中女生甲被选到的概率是多少？
（Ⅱ）能否有95%的把握认为工科院校中“性别”与“专业”有关系？
附：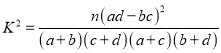 
．
|
|
|
|
|
|
|
|
|
|
|
|
