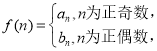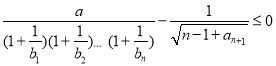题目内容
【题目】记无穷数列![]() 的前
的前![]() 项中最大值为
项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() ,
,![]() .
.
(1)若![]() ,请写出
,请写出![]() 的值;
的值;
(2)求证:“数列![]() 是等差数列”是“数列
是等差数列”是“数列![]() 是等差数列”的充要条件;
是等差数列”的充要条件;
(3)若对任意![]() ,有
,有![]() ,且
,且![]() ,请问:是否存在
,请问:是否存在![]() ,使得对于任意不小于
,使得对于任意不小于![]() 的正整数
的正整数![]() ,有
,有![]() 成立?请说明理由.
成立?请说明理由.
【答案】(1)5;(2)证明见解析;(3)存在,理由见解析.
【解析】
(1)计算得到![]() ,代入计算得到答案.
,代入计算得到答案.
(2)分别证明充分性和必要性得到答案.
(3)反证法,假设不成立,则![]() 或
或![]() 得到
得到![]() ,
,
![]() ,通过累加得到
,通过累加得到![]() ,与题设矛盾,得证.
,与题设矛盾,得证.
(1)(1)![]() ,则
,则![]() ,
,![]()
(2)数列![]() 是等差数列,设公差为
是等差数列,设公差为![]()
则![]() ,
,![]() 为定值,故数列
为定值,故数列![]() 是等差数列;
是等差数列;
数列![]() 是等差数列,设公差为
是等差数列,设公差为![]() ,则
,则![]()
![]() 和
和![]() ,
,![]() 和
和![]() 至少一组相等,不妨设只有
至少一组相等,不妨设只有![]()
则![]() 故
故![]()
故![]() ,
,![]() 为等差数列
为等差数列
同理可得只有![]() 和都相等的情况,故数列
和都相等的情况,故数列![]() 是等差数列
是等差数列
综上所述:“数列![]() 是等差数列”是“数列
是等差数列”是“数列![]() 是等差数列”的充要条件
是等差数列”的充要条件
(3)存在
假设不存在,则![]() 或
或![]() ,对任意
,对任意![]() ,一定存在
,一定存在![]() 使得
使得![]() 符号相反.
符号相反.
所以数列![]() 中存在
中存在![]() ,其中
,其中![]()
且![]() ;
;![]()
因为![]() ,即
,即![]()
注意到:![]() ,有且仅有一个等号成立.
,有且仅有一个等号成立.
所以必有![]()
所以![]() ,所以
,所以![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]()
![]() ;
;![]() ;
;![]() …
…
累加可得![]() ;
;![]()
故![]()
这与![]() 矛盾,假设不成立
矛盾,假设不成立
故存在![]() ,使得对于任意不小于
,使得对于任意不小于![]() 的正整数
的正整数![]() ,有
,有![]() 成立
成立

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.