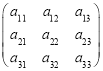题目内容
【题目】将所有平面向量组成的集合记作![]() ,
,![]() 是从
是从![]() 到
到![]() 的映射,记作
的映射,记作![]() 或
或![]() ,其中
,其中![]() 都是实数.定义映射
都是实数.定义映射![]() 的模为:在
的模为:在![]() 的条件下
的条件下![]() 的最大值记做
的最大值记做![]() .若存在非零向量
.若存在非零向量![]() ,及实数
,及实数![]() 使得
使得![]() ,则称
,则称![]() 为
为![]() 的一个特征值.
的一个特征值.
(1)若![]() 求
求![]() ;
;
(2)如果![]() ,计算
,计算![]() 的特征值,并求相应的
的特征值,并求相应的![]() ;
;
(3)试找出一个映射![]() ,满足以下两个条件:①有唯一特征值
,满足以下两个条件:①有唯一特征值![]() ,②
,②![]() .(不需证明)
.(不需证明)
【答案】(1)![]() (2)答案不唯一,具体见解析(3)
(2)答案不唯一,具体见解析(3)![]()
【解析】
(1)根据题目中的定义,在![]() 的条件下
的条件下![]() 的最大值为
的最大值为![]() ,分别用
,分别用![]() 表达
表达![]() 与
与![]() 再分析即可.
再分析即可.
(2) 由![]() 求得
求得![]() 后再联立方程求
后再联立方程求![]() 中
中![]() 的系数.
的系数.
(3)根据题意设![]() ,列出
,列出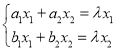 ,再分析
,再分析![]() 满足的关系即可.
满足的关系即可.
(1)由于此时![]() ,
,
又因为是在![]() 的条件下
的条件下![]() (
(![]() 时取最大值),所以此时有
时取最大值),所以此时有![]() ;
;
(2)由![]() ,可得
,可得 :
: ,
,
两式相乘可得:![]() ,从而
,从而![]() .
.
当![]() 时,解方程组
时,解方程组 ,此时这两个方程是同一个方程,
,此时这两个方程是同一个方程,
所以此时方程有无穷多个解,为![]() ,其中
,其中![]() .
.
当![]() 时,同理可得相应的
时,同理可得相应的![]() ,其中
,其中![]() .
.
(3)由方程组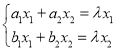 ,可得
,可得![]() 从而向量
从而向量![]() 与
与![]() 平行,从而有
平行,从而有![]() 应满足:
应满足:![]() ;
;
当![]() 时,f有唯一的特征值,且
时,f有唯一的特征值,且![]() ,
,
故![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目