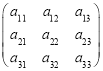题目内容
【题目】
为等差数列，则使等式
能成立的数列的项数
的最大值为_________；
【答案】50
【解析】
根据题意得到数列项数为偶数设为
，根据关系得到
，计算得到关系式
，计算得到答案.
{an}为等差数列，则使等式|a1|+|a2|+…+|an|，
＝|a1+1|+|a2+1|+…+|an+1|，
＝|a1+2|+|a2+2|+…+|an+2|，
＝|a1+3|+|a2+3|+…+|an+3|，
则：数列{an}中的项一定满足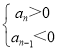
或
，
且项数n为偶数，
设n＝2k，等差数列的公差为d，首项为a1，
不妨设
，
则：a1＜0，d＞0，
且：ak+3＜0，
由
，
可得d＞3，
所以：|a1|+|a2|+..+|an|＝﹣a1﹣a2﹣a3﹣…﹣ak+ak+1+ak+2+…+a2k，
＝﹣2（a1+a2+a3+…+ak）+（a1+a2+a3+…+ak+ak+1+…+a2k）
＝﹣2（
）+（
），
＝k2d＝2018，
由于：d＞3，
所以：k2d＝2018＞3d2，
解得：k2＜672，
故：k≤25，
故：n≤50．
故答案为：50．
练习册系列答案
相关题目
