题目内容
【题目】选修4—4：极坐标与参数方程
在平面直角坐标系
中，将曲线
(
为参数) 上任意一点
经过伸缩变换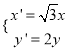
后得到曲线
的图形．以坐标原点
为极点，x轴的非负半轴为极轴，取相同的单位长度建立极坐标系，已知直线
．
（Ⅰ）求曲线
和直线
的普通方程；
（Ⅱ）点P为曲线
上的任意一点，求点P到直线
的距离的最大值及取得最大值时点P的坐标．
【答案】（1）
, 
（2）
，P
【解析】试题分析：（I）根据伸缩变换的公式代入原方程,可以得到伸缩后的曲线方程；
（II）利用点P在椭圆上设出参数坐标,根据点到直线的距离公式求三角函数的最值,并求出取得最值时的
值.
试题解析：（I）由已知有
（
为参数），消去
得
．
将
代入直线
的方程得
曲线
的方程为
，直线
的普通方程为
.
（II）由（I）可设点
为
， 
．则点
到直线
的距离为：
故当
，即
时
．
此时点
的坐标为
．
练习册系列答案
相关题目
【题目】据统计，2017年国庆中秋假日期间，黔东南州共接待游客590.23万人次，实现旅游收入48.67亿元，同比分别增长44.57%、55.22%.旅游公司规定：若公司导游接待旅客，旅游年总收入不低于40（单位：百万元），则称为优秀导游.经验表明，如果公司的优秀导游率越高，则该公司的影响度越高.已知甲、乙两家旅游公司各有导游100名，统计他们一年内旅游总收入，分别得到甲公司的频率分布直方图和乙公司的频数分布表如下：
分组 |
|
|
|
|
|
频数 |
| 18 | 49 | 24 | 5 |
（Ⅰ）求
的值，并比较甲、乙两家旅游公司，哪家的影响度高?
（Ⅱ）若导游的奖金
（单位：万元），与其一年内旅游总收入
（单位：百万元）之间的关系为
，求甲公司导游的年平均奖金；
（Ⅲ）从甲、乙两家公司旅游收入在
的总人数中，用分层抽样的方法随机抽取6人进行表彰，其中有两名导游代表旅游行业去参加座谈，求参加座谈的导游中有乙公司导游的概率.
