题目内容
20.将函数y=sin(x+$\frac{π}{6}$)图象上所有点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再把所得图象向右平移$\frac{π}{6}$个单位后得到函数y=f(x)的图象,则函数y=f(x)的图象( )| A. | 关于点(0,0)对称 | B. | 关于点($\frac{π}{4}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{3}$对称 | D. | 关于直线x=π对称 |
分析 利用三角函数图象之间的关系进行判断即可.
解答 解:将函数y=sin(x+$\frac{π}{6}$)图象上所有点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),
得到y=sin(2x+$\frac{π}{6}$),
再把所得图象向右平移$\frac{π}{6}$个单位后得到y=sin[2(x-$\frac{π}{6}$)+$\frac{π}{6}$]=sin(2x-$\frac{π}{6}$),
即f(x)=sin(2x-$\frac{π}{6}$),
则f(0)=sin(-$\frac{π}{6}$)=-$\frac{1}{2}≠0$,即函数关于(0,0)不对称,
f($\frac{π}{4}$)=sin(2×$\frac{π}{4}$-$\frac{π}{6}$)=sin($\frac{π}{2}-\frac{π}{6}$)=cos$\frac{π}{6}$≠0,即关于点($\frac{π}{4}$,0)不对称,
f($\frac{π}{3}$)=sin(2×$\frac{π}{3}$-$\frac{π}{6}$)=sin$\frac{π}{2}$=1,即关于直线x=$\frac{π}{3}$对称,故C正确,
故选:C.
点评 根据三角函数图象之间的关系求出函数的解析式,利用三角函数的对称性进行判断即可.

练习册系列答案
相关题目
10.过定点P(0,2)作直线l,使l与曲线y2=4x有且仅有1个公共点,这样的直线l共有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
5.已知m=0.91.1,n=1.10.9,p=log0.91.1,则m、n、p的大小关系( )
| A. | m<n<p. | B. | m<p<n | C. | p<m<n | D. | p<n<m |
12.如果执行右边的程序框图,若输入x=-11,那么其输出的结果是( )
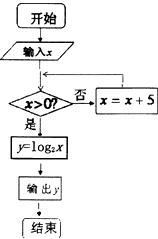

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
9.已知集合A={x|-1≤x≤1},B={x|x2-5x+6≥0},则下列结论中正确的是( )
| A. | A∩B=B | B. | A∪B=A | C. | A?B | D. | ∁RA=B |
10.设Sn为等比数列{an}的前n项和,若8a3+a6=0,则$\frac{{S}_{6}}{{S}_{2}}$=( )
| A. | -11 | B. | -21 | C. | 11 | D. | 21 |
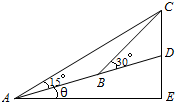 米到达B点,再次测量得其斜度为30°,假设建筑物高50米,设山坡对于水平面的斜度为θ,则cosθ=$\frac{3}{4}$.
米到达B点,再次测量得其斜度为30°,假设建筑物高50米,设山坡对于水平面的斜度为θ,则cosθ=$\frac{3}{4}$.