题目内容
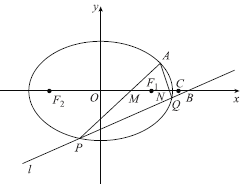
【题目】如图,点![]() 在以
在以![]() 为焦点的双曲线
为焦点的双曲线![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,若四边形
,若四边形![]() 为菱形,则该双曲线的离心率为( )
为菱形,则该双曲线的离心率为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
【答案】C
【解析】
连接![]() ,可得三角形
,可得三角形![]() 为等边三角形,过点P作PH⊥x轴于点H, 则∠
为等边三角形,过点P作PH⊥x轴于点H, 则∠![]() =60
=60![]() ,可得
,可得![]() |=2c, , |
|=2c, , |![]() |=
|=![]() , |
, |![]() |=
|=![]() ,连接
,连接![]() ,利用双曲线的性质, 2a=|
,利用双曲线的性质, 2a=|![]() |-|
|-|![]() |=
|=![]() -2c=
-2c=![]() ,可得离心率e.
,可得离心率e.
解:由题意得:
四边形![]() 的边长为2c, 连接
的边长为2c, 连接![]() ,由对称性可知, |
,由对称性可知, |![]() |=|
|=|![]() |=2c,则三角形
|=2c,则三角形![]() 为等边三角形.
为等边三角形.
过点P作PH⊥x轴于点H, 则∠![]() =60
=60![]() ,
,
![]() |
|![]() |=2c,
|=2c,![]() 在直角三角形
在直角三角形![]() 中, |
中, |![]() |=
|=![]() , |
, |![]() |=
|=![]() ,
,
则P(2c,![]() ), 连接
), 连接![]() , 则|
, 则|![]() |=
|=![]() .
.
由双曲线的定义知,2a=|![]() |-|
|-|![]() |=
|=![]() -2c=
-2c=![]() ,
,
所以双曲线的离心率为e=![]() =
=![]() =
=![]() ,
,
故选C.

练习册系列答案
相关题目
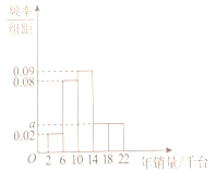
【题目】为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间![]() (单位:小时),整理得到数据分组及频率分布直方图如下:
(单位:小时),整理得到数据分组及频率分布直方图如下:

组号 | 分组 | 频数 |
1 |
| 6 |
2 |
| 8 |
3 |
| 22 |
4 |
| 28 |
5 |
| 12 |
6 |
| 4 |
(1)从该单位随机选取一名职工,试计算这名职工一周内路边停车的时间少于8小时的频率;
(2)求频率分布直方图中![]() 的值.
的值.