题目内容
【题目】如图，在三棱柱
中，四边形
是菱形，四边形
是正方形，
，
，
，点
为
的中点.
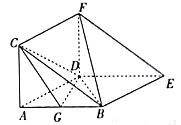
（1）求证：
平面
；
（2）求点
到平面的距离.
【答案】（1）见解析；（2）
.
【解析】
（1）连接AF，与CD交于点H，连接GH，由中位线定理可得BF∥GH，从而得证；
（2）由点H为AF的中点，可知点F到平面CDG的距离与点A到平面CDG的距离相等，再利用
，即可得解.
(1)连接AF，与CD交于点H，连接GH，
则GH为△ABF的中位线，
所以BF∥GH，
又BF
平面CDG，GH平面CDG，
所以BF∥平面CDG.
(2)由点H为AF的中点，且点
平面CDG可知，
点F到平面CDG的距离与点A到平面CDG的距离相等，
由四边形
是正方形，
，可得
是三棱锥
的高，
由题意得，
，
所以
，
在△CDG中，
，
设点A到平面CDG的距离为h，则
，
由得，
，
所以点F到平面CDG的距离为.
ABC考王全优卷系列答案【题目】随着“互联网+交通”模式的迅猛发展，“共享自行车”在很多城市相继出现。某运营公司为了了解某地区用户对其所提供的服务的满意度，随机调查了40个用户，得到用户的满意度评分如下：
用户编号 | 评分 | 用户编号 | 评分 | 用户编号 | 评分 | 用户编号 | 评分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系统抽样法从40名用户中抽取容量为10的样本，且在第一分段里随机抽到的评分数据为92.
（1）请你列出抽到的10个样本的评分数据；
（2）计算所抽到的10个样本的均值
和方差
；
（3）在（2）条件下，若用户的满意度评分在
之间，则满意度等级为“
级”。试应用样本估计总体的思想，根据所抽到的10个样本，估计该地区满意度等级为“
级”的用户所占的百分比是多少？
（参考数据：
）
