题目内容
【题目】已知 
， 
，函数f（x）= 
．
（Ⅰ）求函数y=f（x）图象的对称轴方程；
（Ⅱ）若方程f（x）= 
在（0，π）上的解为x1 ， x2 ， 求cos（x1﹣x2）的值．
【答案】解：（Ⅰ） 
= 
，
令 
，得 
，
即y=f（x）的对称轴方程为 
，（k∈Z）．
（Ⅱ）由条件知 
，且 
，
易知（x1 ， f（x1））与（x2 ， f（x2））关于 
对称，则 
，
∴ 
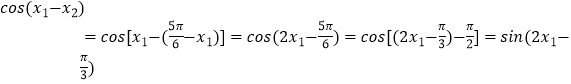
【解析】（Ⅰ）由已知利用平面向量数量积的运算，三角函数恒等变换的应用化简可得函数解析式为f（x）=sin（2x﹣ 
），利用正弦函数的对称性即可得解．（Ⅱ）由条件知 ，且 ，可求 ，利用诱导公式即可化简求值得解．
【考点精析】关于本题考查的两角和与差的余弦公式，需要了解两角和与差的余弦公式：
才能得出正确答案．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
【题目】已知函数f（x）=|x﹣a|，其中a＞1
（1）当a=2时，求不等式f（x）≥4﹣|x﹣4|的解集；
（2）已知关于x的不等式|f（2x+a）﹣2f（x）|≤2的解集{x|1≤x≤2}，求a的值．
【题目】某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
（1）画出散点图；
（2）求回归直线方程；
（3）据此估计广告费用为12万元时，销售收入y的值．
