题目内容
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1.M是棱SB的中点.
(Ⅰ)求证:AM∥面SCD;
(Ⅱ)求面SCD与面SAB所成二面角的余弦值;
(Ⅲ)设点N是直线CD上的动点,MN与面SAB所成的角为θ,求sinθ的最大值.
【答案】解:(Ⅰ)以点A为原点建立如图所示的空间直角坐标系,
则A(0,0,0),B(0,2,0),D(1,0,0,),S(0,0,2),M(0,1,1).
则 ![]() ,
, ![]() ,
, ![]() .
.
设平面SCD的法向量是 ![]() ,则
,则  ,即
,即 ![]()
令z=1,则x=2,y=﹣1.于是 ![]() .
.
∵ ![]() ,∴
,∴ ![]() .
.
又∵AM平面SCD,∴AM∥平面SCD.
(Ⅱ)易知平面SAB的法向量为 ![]() .设平面SCD与平面SAB所成的二面角为α,
.设平面SCD与平面SAB所成的二面角为α,
则 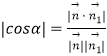 =
= ![]() =
= ![]() ,即
,即 ![]() .
.
∴平面SCD与平面SAB所成二面角的余弦值为 ![]() .
.
(Ⅲ)设N(x,2x﹣2,0),则 ![]() .
.
∴  =
= ![]() =
= ![]() =
= ![]() .
.
当 ![]() ,即
,即 ![]() 时,
时, ![]() .
.
【解析】(Ⅰ)通过建立空间直角坐标系,利用平面SCD的法向量 ![]() 即可证明AM∥平面SCD;(Ⅱ)分别求出平面SCD与平面SAB的法向量,利用法向量的夹角即可得出;(Ⅲ)利用线面角的夹角公式即可得出表达式,进而利用二次函数的单调性即可得出.
即可证明AM∥平面SCD;(Ⅱ)分别求出平面SCD与平面SAB的法向量,利用法向量的夹角即可得出;(Ⅲ)利用线面角的夹角公式即可得出表达式,进而利用二次函数的单调性即可得出.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目

