题目内容
3.(1)已知sin(x+$\frac{7π}{6}$)=-$\frac{1}{4}$,求sin($\frac{7π}{6}$+x)+cos2($\frac{23π}{6}-x$)的值;(2)已知cos(α+β)+1=0,求证:sin(2α+β)+sinβ=0.
分析 (1)sin(x+$\frac{7π}{6}$)=-$\frac{1}{4}$,可得$sin(x+\frac{π}{6})$=$\frac{1}{4}$.cos2($\frac{23π}{6}-x$)=$co{s}^{2}(\frac{π}{6}+x)$=1-$si{n}^{2}(\frac{π}{6}+x)$,代入即可得出.
(2)由cos(α+β)+1=0,可得sin(α+β)=0.于是sin(2α+β)+sinβ=sin[(α+β)+α]+sin[(α+β)-α],展开即可得出.
解答 (1)解:∵sin(x+$\frac{7π}{6}$)=-$\frac{1}{4}$,
∴$sin(x+\frac{π}{6})$=$\frac{1}{4}$.
∴sin($\frac{7π}{6}$+x)+cos2($\frac{23π}{6}-x$)
=-$\frac{1}{4}$+$co{s}^{2}(\frac{π}{6}+x)$
=-$\frac{1}{4}$+1-$si{n}^{2}(\frac{π}{6}+x)$
=$\frac{3}{4}-(-\frac{1}{4})^{2}$
=$\frac{11}{16}$.
(2)证明:∵cos(α+β)+1=0,
∴sin(α+β)=0.
∴sin(2α+β)+sinβ=sin[(α+β)+α]+sin[(α+β)-α]
=2sin(α+β)cosα=0,
∴sin(2α+β)+sinβ=0.
点评 本题考查了诱导公式、同角三角函数基本关系式、和差公式,考查了变形能力、推理能力与计算能力,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
14.已知α为第三象限角,则tan$\frac{α}{2}$的值( )
| A. | 一定为正数 | B. | 一定为负数 | ||
| C. | 可能为正数,也可能为负数 | D. | 不存在 |
18.若关于x的方程(log2x)2+2alog2x+1=0有大于1的实数解,则实数a的取值范围是( )
| A. | (-∞,-1] | B. | [1,+∞) | C. | (1,+∞) | D. | (-∞,-1]∪[1,+∞) |
15.不等式2+log0.5(5-x)+log2$\frac{1}{x}$>0的解集是( )
| A. | (0,+∞) | B. | (-∞,5) | C. | (0,1)∪(4,5) | D. | 空集 |
 已知,如图所示.
已知,如图所示.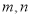 表示两条不同直线,
表示两条不同直线,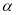 表示平面.下列说法正确的是
表示平面.下列说法正确的是 则
则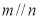 B.若
B.若 ,则
,则
 则
则 D.若
D.若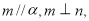 ,则
,则