题目内容
12.已知a,b∈R,命题p:a=b,命题q:($\frac{a+b}{2}$)2≤$\frac{{a}^{2}+{b}^{2}}{2}$,那么在命题“若p,则q”及其逆命题、否命题、逆否命题中真命题的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 根据四种命题的定义以及命题真假之间的关系进行判断即可.
解答 解:命题p:a=b,命题q:($\frac{a+b}{2}$)2≤$\frac{{a}^{2}+{b}^{2}}{2}$,
若p,则q正确,∴原命题正确,则逆否命题也正确.
若:($\frac{a+b}{2}$)2≤$\frac{{a}^{2}+{b}^{2}}{2}$,则($\frac{a-b}{2}$)2≥0,对于a,b∈R都可以,
命题为:若q,则p不正确,
∴逆命题为假命题,则否命题也为假命题,
∴真命题的个数是2个,
故选:C.
点评 本题主要考查四种命题之间的关系以及逆否命题的等价性问题,利用逆否命题的等价性是解决本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
20.不等式23x-1>$\frac{\sqrt{2}}{2}$的解集是( )
| A. | (1,+∞) | B. | ($\frac{1}{6}$,+∞) | C. | (-∞,1) | D. | ($\frac{3}{2}$,+∞) |
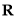 上的函数
上的函数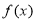 满足
满足 且
且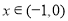 时,
时,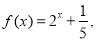 则
则 __________.
__________.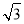 m以后测得山峰的仰角为4θ,求该山峰的高度
m以后测得山峰的仰角为4θ,求该山峰的高度