题目内容
18.在△ABC中,已知b=2,a=$\frac{{2\sqrt{3}}}{3},A={30°}$,求角B,C及边c.分析 根据题意和正弦定理求出sinB,由内角的范围和特殊角的正弦值求出B,再分别由内角和定理求出C以及边c.
解答 解:由题意知,b=2,a=$\frac{{2\sqrt{3}}}{3},A={30°}$,
根据正弦定理得,$\frac{a}{sinA}=\frac{b}{sinB}$,
则sinB=$\frac{bsinA}{a}$=$\frac{2×\frac{1}{2}}{\frac{2\sqrt{3}}{3}}$=$\frac{\sqrt{3}}{2}$,
由0<B<180°,则B=60°或120°,
①当B=60°时,C=180°-A-B=90°,
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{4+\frac{12}{9}}$=$\frac{4\sqrt{3}}{3}$,
②当B=120°时,C=180°-A-B=30°,
∴A=C,则c=a=$\frac{2\sqrt{3}}{3}$.
点评 本题考查正弦定理在解三角形中的应用,以及内角和定理,注意角的范围,属于中档题.

练习册系列答案
相关题目
3.化简:sin($\frac{4n-1}{4}$π-α)+cos($\frac{4n+1}{4}$π-α)(n∈Z)值( )
| A. | 2sinа | B. | 2cosа | C. | 0 | D. | -2sinа |
10.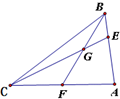 如图,在△ABC中,BE:EA=1:2,F是AC中点,线段CE与BF交于点G,则△BEG的面积与△ABC的面积之比是( )
如图,在△ABC中,BE:EA=1:2,F是AC中点,线段CE与BF交于点G,则△BEG的面积与△ABC的面积之比是( )
 如图,在△ABC中,BE:EA=1:2,F是AC中点,线段CE与BF交于点G,则△BEG的面积与△ABC的面积之比是( )
如图,在△ABC中,BE:EA=1:2,F是AC中点,线段CE与BF交于点G,则△BEG的面积与△ABC的面积之比是( )| A. | $\frac{1}{16}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
8.已知平面中三点A(-1,-1),B(1,2),C(8,-2),判断三角形ABC的形状( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法判断 |