题目内容
6.已知(1+ax)(1+x)5的展开式中x2的系数为5,则a=-1.分析 根据x2产生的两种可能分别得到其系数的等式解出a.
解答 解:因为(1+ax)(1+x)5的展开式中x2的系数为5,则${C}_{5}^{2}+a{C}_{5}^{1}$=5,即10+5a=5,解得a=-1;
故答案为:-1.
点评 本题考查了二项式定理的运用;关键是明确x2项产生的可能,计算系数.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
17.判断两个分类变量时彼此相关还是相互独立的常用方法中,最为精确的是( )
| A. | 2×2列联表 | B. | 独立性检验 | C. | 登高条形图 | D. | 其他 |
16.10个篮球队中有2个强队,先任意将这10个队平均分成两组进行比赛,则2个强队不分在同一组的概率是 ( )
| A. | $\frac{5}{18}$ | B. | $\frac{5}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
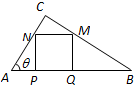 如图,某单位准备绿化一块直径AB=a的半圆形空地,△ABC以外地方种草,△ABC的内接正方形PQMN为一水池,其余的地方种花,设∠BAC=θ,△ABC的面积为S1,正方形PQMN的面积为S2.
如图,某单位准备绿化一块直径AB=a的半圆形空地,△ABC以外地方种草,△ABC的内接正方形PQMN为一水池,其余的地方种花,设∠BAC=θ,△ABC的面积为S1,正方形PQMN的面积为S2.