题目内容
(本题12分)已知函数f (x)=x 2+ax ,且对任意的实数x都有f (1+x)=f (1-x) 成立.
(1)求实数 a的值;
(2)利用单调性的定义证明函数f(x)在区间[1,+∞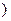 上是增函数.
上是增函数.
(1)求实数 a的值;
(2)利用单调性的定义证明函数f(x)在区间[1,+∞
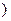 上是增函数.
上是增函数.(1)a=-2.
(2) 略
(2) 略
解:(1)由f (1+x)=f (1-x)得,
(1+x)2+a(1+x)=(1-x)2+a(1-x),
整理得:(a+2)x=0,
由于对任意的x都成立,∴a=-2. ----------------------------------------(6分)

(1+x)2+a(1+x)=(1-x)2+a(1-x),
整理得:(a+2)x=0,
由于对任意的x都成立,∴a=-2. ----------------------------------------(6分)


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
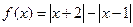 .
.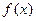 的值域;
的值域;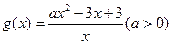 若对
若对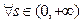 ,
, 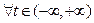 ,恒
,恒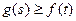 成立,试求实数
成立,试求实数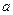 的取值范围
的取值范围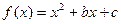 ,对于任意的
,对于任意的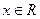 ,恒有
,恒有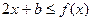 .
.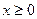 时,
时,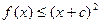 ;
;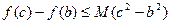 恒成立,求
恒成立,求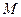 的最小值.
的最小值.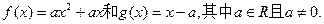
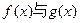 的图象的一个公共点恰好在x轴上,求a的值;
的图象的一个公共点恰好在x轴上,求a的值;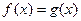 的两根,且满足
的两根,且满足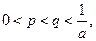 证明:
证明: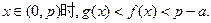

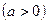 ,方程
,方程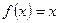 的两个根为
的两个根为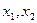 ,
,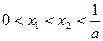 ,那么当
,那么当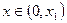 时,
时,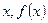 与
与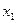 的大小关系为( )
的大小关系为( )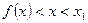 B
B 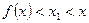 C
C 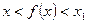 D
D 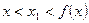
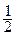 , 函数y=x(1–2x)的最大值是( )
, 函数y=x(1–2x)的最大值是( )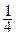
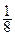

 值
值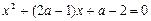 的一根比1大,另一根比-1小,则实数a的取值范围是 .
的一根比1大,另一根比-1小,则实数a的取值范围是 .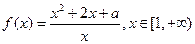
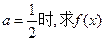 的最小值。(2)若对任
的最小值。(2)若对任 意
意
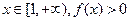 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。