题目内容
(本小题8分)
设函数f(x)=x2-2x+2 ,x∈[t,t+1],t∈R,求函数f(x)的最小值g(t)的表达式.
设函数f(x)=x2-2x+2 ,x∈[t,t+1],t∈R,求函数f(x)的最小值g(t)的表达式.
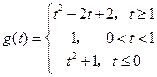
解:当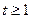 时,
时,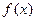 在
在 上是增函数,
上是增函数,
当 时,
时,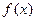 在
在 上是减函数,∴
上是减函数,∴ ,
,
当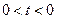 时,
时,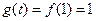
∴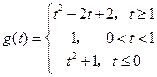
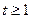 时,
时,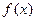 在
在 上是增函数,
上是增函数,
当
 时,
时,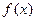 在
在 上是减函数,∴
上是减函数,∴ ,
,当
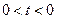 时,
时,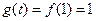
∴
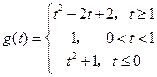

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
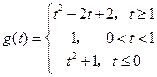
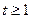 时,
时,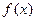 在
在 上是增函数,
上是增函数,
 时,
时,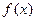 在
在 上是减函数,∴
上是减函数,∴ ,
,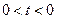 时,
时,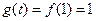
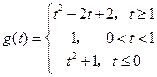

 阅读快车系列答案
阅读快车系列答案