题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{4}x|,0<x≤4}\\{{x}^{2}-10x+25,x>4}\end{array}\right.$,若a,b,c,d互不相等,且f(a)=f(b)=f(c)=f(d),则abcd的取值范围为( )| A. | [24,25] | B. | (24,25) | C. | (0,25) | D. | [0,25] |
分析 画出函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{4}x|,0<x≤4}\\{{x}^{2}-10x+25,x>4}\end{array}\right.$的图象,根据a,b,c,d互不相等,且f(a)=f(b)=f(c)=f(d),我们令a<b<c<d,我们易根据对数的运算性质,及c,d的取值范围得到abcd的取值范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{4}x|,0<x≤4}\\{{x}^{2}-10x+25,x>4}\end{array}\right.$的图象如下图所示:
若a,b,c,d互不相等,且f(a)=f(b)=f(c)=f(d),
不妨令a<b<c<d,
则log4a+log4=log4ab=0,即ab=1,
c+d=10,c∈(4,5),d∈(5,6),
则cd∈(24,25).
故abcd∈(24,25).
故选:B
点评 本题考查的知识点是对数函数图象与性质的综合应用,其中画出函数图象,利用图象的直观性,数形结合进行解答是解决此类问题的关键.

练习册系列答案
相关题目
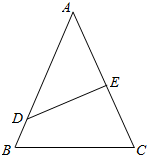 某校把一块形状为正三角形的边角地ABC开辟为生态园,如图所示,其中AB=2a,DE把三角形分成面积相等的两个部分,D在线段AB上,E在线段AC上.
某校把一块形状为正三角形的边角地ABC开辟为生态园,如图所示,其中AB=2a,DE把三角形分成面积相等的两个部分,D在线段AB上,E在线段AC上.