题目内容
12.若曲线y=x2-aln(x+1)在x=1处取极值,则实数a的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 求出函数的导函数,由f′(1)=0求得a的值,注意要检验.
解答 解:定义域为(-1,+∞)
y′=2x-$\frac{a}{x+1}$,当x=1时,2-$\frac{a}{2}$=0,得a=4,
当a=4时,${y}^{′}=2x-\frac{4}{x+1}$=$2\frac{{x}^{2}+x-2}{x+1}=\frac{2(x-1)(x+2)}{x+1}$
∴函数在(-1,1)上单调递减,在(1,+∞)上单调递增,即a=4时符合题意.
故选D.
点评 本题是一道导数的应用题,考查了导函数的零点与极值的关系.属于基础题.

练习册系列答案
相关题目
8.为得到函数y=sin(x+$\frac{π}{6}$)的图象,可将函数y=sinx的图象向左平移m个单位长度,或向右平移n个单位长度(m,n均为正数,则|m-n|的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
20.有下列命题是假命题的是:( )
| A. | 双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1与椭圆$\frac{{x}^{2}}{35}$+y2=1有相同的焦点 | |
| B. | “0<x<2”是“x2-2x-3<0”充分不必要条件 | |
| C. | “若xy=0,则x、y中至少有一个为0”的否命题是真命题. | |
| D. | “?x∈R,使x2-2x+3≤0” |
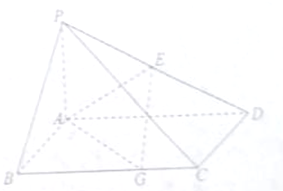 如图,在四棱锥P-ABCD中,底圆ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,点G在线段BC上,且BG=3.
如图,在四棱锥P-ABCD中,底圆ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,点G在线段BC上,且BG=3. 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.则异面直线OB与MD所成角余弦值为$\frac{\sqrt{10}}{10}$.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.则异面直线OB与MD所成角余弦值为$\frac{\sqrt{10}}{10}$.