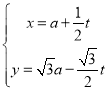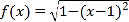题目内容
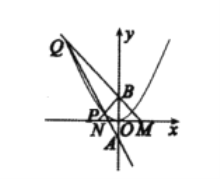
【题目】如图,直线![]() 与y轴交于点A,与抛物线
与y轴交于点A,与抛物线![]() 交于P,Q,点B与点A关于x轴对称,连接QB,BP并延长分别与x轴交于点M,N.
交于P,Q,点B与点A关于x轴对称,连接QB,BP并延长分别与x轴交于点M,N.
(1)若![]() ,求抛物线C的方程;
,求抛物线C的方程;
(2)若![]() ,求
,求![]() 外接圆的方程.
外接圆的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)联立![]() 可得
可得![]() ,
,
设点![]() ,
,![]() ,由
,由![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,
,
表示出![]() .利用
.利用![]() ,可得
,可得![]() ,即可可得到抛物线方程;
,即可可得到抛物线方程;
(2)设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() 点,由
点,由![]() ,
,![]() ,
,
可得![]() .则直线
.则直线![]() 的方程为:
的方程为:![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,由此可得
,由此可得![]() ,结合
,结合![]() 可得,
可得,![]() ,∴
,∴![]() ,且
,且![]() ,故
,故![]() ,
,
即![]() 是等腰三角形,且
是等腰三角形,且![]() ,则
,则![]() 的外接圆的圆心一定在y轴上,设为
的外接圆的圆心一定在y轴上,设为![]() ,由圆心到点M,B的距离相等可解得
,由圆心到点M,B的距离相等可解得![]() ,于是得到外接圆方程.
,于是得到外接圆方程.
(1)由![]() 可得
可得![]() ,
,
设点![]() ,
,![]() ,则
,则![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,
故![]() .
.
由![]() 可得
可得![]() (舍去负值),
(舍去负值),
∴抛物线C的方程为![]() .
.
(2)设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() 点,
点,
 ,
,
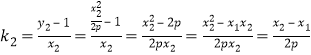 ,
,
∴![]() .
.
直线![]() 的方程为:
的方程为:![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,由
,由![]() 可得
可得![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,且
,且![]() ,故
,故![]() ,
,
即![]() 是等腰三角形,且
是等腰三角形,且![]() ,则
,则![]() 的外接圆的圆心一定在y轴上,设为
的外接圆的圆心一定在y轴上,设为![]() ,由圆心到点M,B的距离相等可得
,由圆心到点M,B的距离相等可得![]() ,解之得
,解之得![]() ,外接圆方程为
,外接圆方程为![]() .
.

练习册系列答案
相关题目