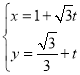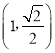题目内容
【题目】设![]() 是定义在R上的两个周期函数,
是定义在R上的两个周期函数,![]() 的周期为4,
的周期为4,![]() 的周期为2,且
的周期为2,且![]() 是奇函数.当
是奇函数.当![]() 时,
时,![]() ,
,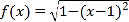 ,其中k>0.若在区间(0,9]上,关于x的方程
,其中k>0.若在区间(0,9]上,关于x的方程![]() 有8个不同的实数根,则k的取值范围是_____.
有8个不同的实数根,则k的取值范围是_____.
【答案】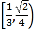 .
.
【解析】
分别考查函数![]() 和函数
和函数![]() 图像的性质,考查临界条件确定k的取值范围即可.
图像的性质,考查临界条件确定k的取值范围即可.
当![]() 时,
时,![]() 即
即![]()
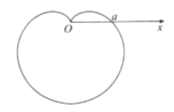
又![]() 为奇函数,其图象关于原点对称,其周期为4,如图,函数
为奇函数,其图象关于原点对称,其周期为4,如图,函数![]() 与
与![]() 的图象,要使
的图象,要使![]() 在(0,9]上有8个实根,只需二者图象有8个交点即可.
在(0,9]上有8个实根,只需二者图象有8个交点即可.
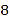
当![]() 时,函数
时,函数![]() 与
与![]() 的图象有2个交点;
的图象有2个交点;
当![]() 时,
时,![]() 的图象为恒过点(-2,0)的直线,只需函数
的图象为恒过点(-2,0)的直线,只需函数![]() 与
与![]() 的图象有6个交点.当
的图象有6个交点.当![]() 与
与![]() 图象相切时,圆心(1,0)到直线
图象相切时,圆心(1,0)到直线![]() 的距离为1,即
的距离为1,即![]() ,得
,得![]() ,函数
,函数![]() 与
与![]() 的图象有3个交点;当
的图象有3个交点;当![]() 过点(1,1)时,函数
过点(1,1)时,函数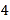 与
与![]() 的图象有6个交点,此时
的图象有6个交点,此时![]() ,得
,得![]() .
.
综上可知,满足![]() 在(0,9]上有8个实根的k的取值范围为
在(0,9]上有8个实根的k的取值范围为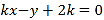 .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目