题目内容
3.设中心在坐标原点的椭圆左、右两个焦点分别为F1、F2,过F2的一条直线与该椭圆相交于A、B两点,已知等边三角形ABF1的边长为4.求该椭圆的方程.分析 确定AB⊥F1F2,利用等边三角形ABF1的边长为4,求出a,b,c,即可得到椭圆的方程.
解答 解:由题意,AB⊥F1F2,
∵等边三角形ABF1的边长为4,
∴|F1F2|=2c=2$\sqrt{3}$,$\frac{2{b}^{2}}{a}$=4,
∴c=$\sqrt{3}$,a=3,
∴b=$\sqrt{6}$,
∴椭圆的方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{6}=1$.
点评 本题考查椭圆的方程,考查椭圆的性质,考查学生的计算能力,比较基础.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
15.已知数列{an}满足a1=1,an=logn(n+1)(n≥2,n∈N*).定义:使乘积a1•a2•a3…an为正整数的k(k∈N+)叫做“幸运数”,则在[1,2015]内所有“幸运数”的和为( )
| A. | 2035 | B. | 2036 | C. | 4084 | D. | 4085 |
16.已知向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为θ,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则θ的取值范围是( )
| A. | $\frac{π}{6}≤θ≤\frac{π}{2}$ | B. | $\frac{π}{3}≤θ≤\frac{π}{2}$ | C. | $0≤θ≤\frac{π}{3}$ | D. | $0<θ<\frac{2π}{3}$ |
 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.
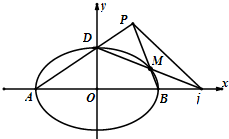
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$. 已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.
已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.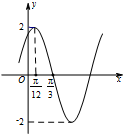 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.