题目内容
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,在
,在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,四边形
的中点,四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() .
.

(Ⅰ)求异面直线![]() 与
与![]() 所成角的正弦值;
所成角的正弦值;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析;(Ⅲ)
;(Ⅱ)证明见解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)因为![]() //
//![]() ,则
,则![]() 即为所求,解三角形即可容易求得;
即为所求,解三角形即可容易求得;
(Ⅱ)先证![]() 平面
平面![]() ,即可求线面垂直推证面面垂直;
,即可求线面垂直推证面面垂直;
(Ⅲ)由(Ⅱ)中所证,即可知![]() 即为所求,再解三角形即可求得结果.
即为所求,再解三角形即可求得结果.
(Ⅰ)因为四边形![]() 是等腰梯形,故可得
是等腰梯形,故可得![]() //
//![]() ,
,
故![]() 即为所求夹角或其补角,
即为所求夹角或其补角,
在![]() 中,因为
中,因为![]() ,且
,且![]() 为底边
为底边![]() 中点,
中点,
故可得![]() ,又因为
,又因为![]() ,
,
故可得![]() ,
,
则![]() .
.
故异面直线![]() 与
与![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅱ)因为平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
又因为![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,故可得
,故可得![]() ;
;
又在四边形![]() 中:过
中:过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
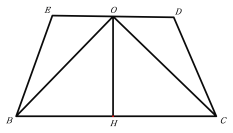
因为![]() ,
,
故容易得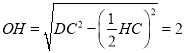 ,
,
则![]()
满足![]() ,则
,则![]() ;
;
又因为![]() 平面
平面![]() ,且
,且![]() ,
,
故可得![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]() ,即证.
,即证.
(Ⅲ)由(Ⅱ)可得![]() 平面
平面![]() ,
,
则![]() 即为所求线面角.
即为所求线面角.
在![]() 中,因为
中,因为![]() ,
,
故可得![]() .
.
故直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】红外线治疗仪的治疗作用是在红外线照射下,组织温度升高,毛细血管扩张,血流加快,物质代谢增强,组织细胞活力及再生能力提高,对我们身体某些疾病的治疗有着很大的贡献,某药店兼营某种红外线治疗仪,经过近![]() 个月的营销,对销售状况进行相关数据分析,发现月销售量与销售价格有关,其统计数据如下表:
个月的营销,对销售状况进行相关数据分析,发现月销售量与销售价格有关,其统计数据如下表:
每台红外线治疗仪的销售价格: |
|
|
|
|
|
红外线治疗仪的月销售量: |
|
|
|
|
|
(1)根据表中数据求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)①每台红外线治疗仪的价格为![]() 元时,预测红外线治疗仪的月销售量;(四舍五入为整数)
元时,预测红外线治疗仪的月销售量;(四舍五入为整数)
②若该红外线治疗仪的成本为![]() 元/台,药店为使每月获得最大的纯收益,利用(1)中结论,问每台该种红外线治疗仪的销售价格应定为多少元?(四舍五入,精确到
元/台,药店为使每月获得最大的纯收益,利用(1)中结论,问每台该种红外线治疗仪的销售价格应定为多少元?(四舍五入,精确到![]() 元).
元).
参考公式:回归直线方程![]() ,
,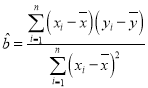 ,
,![]() .
.
【题目】光伏发电是将光能直接转变为电能的一种技术,具有资源的充足性及潜在的经济性等优点,在长期的能源战略中具有重要地位,2015年起,国家能源局、国务院扶贫办联合在6省的30个县开展光伏扶贫试点,在某县居民中随机抽取50户,统计其年用量得到以下统计表.以样本的频率作为概率.
用电量(单位:度) |
|
|
|
|
|
户数 | 7 | 8 | 15 | 13 | 7 |
(Ⅰ)在该县居民中随机抽取10户,记其中年用电量不超过600度的户数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(Ⅱ)在总结试点经验的基础上,将村级光伏电站稳定为光伏扶贫的主推方式.已知该县某自然村有居民300户.若计划在该村安装总装机容量为300千瓦的光伏发电机组,该机组所发电量除保证该村正常用电外,剩余电量国家电网以0.8元/度的价格进行收购.经测算每千瓦装机容量的发电机组年平均发电1000度,试估计该机组每年所发电量除保证正常用电外还能为该村创造直接受益多少元?
