Question

【题目】已知定义在R上奇函数f(x)在时的图象是如图所示的抛物线的一部分.

（1）请补全函数f(x)的图象；

（2）写出函数f(x)的表达式；

（3）讨论方程|f(x)|=a的解的个数.

Answer 1

【答案】（1）答案见解析；（2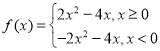）；（3）答案见解析.

【解析】

（1）利用奇函数关于原点对称可得图象；

（2）时，函数图象为抛物线的一部分，顶点在，且过原点利用抛物线的顶点式写出其解析式即可，根据奇函数性质即可求得f(x)的表达式；

（3）方程|f(x)|=a的解的个数，即函数|f(x)|的图象和直线y=a的交点个数，数形结合即可得出结果.

解：（1）补全f(x)的图象如图所示：

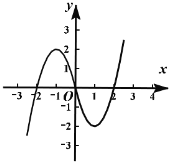
（2）当时，设，由f(0)=0得，a=2，

所以此时，.

当x<0时，x>0，所以①

又f(x)=f(x)，代入①得

综上可得，.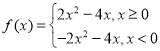

（3）方程|f(x)|=a的解的个数，即函数|f(x)|的图象和直线y=a的交点个数，函数y=|f(x)|的图象如图2所示，

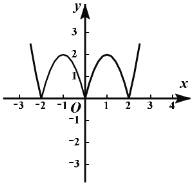
由图象可得，当a<0时，方程无解；当a=0时，方程有三个解；

当0<a<2时，方程有6个解；当a=2时，方程有4个解；当a>2时，方程有2个解.