题目内容
15.在同一坐标系中,将椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1变换成单位圆的伸缩变换是( )| A. | φ:$\left\{\begin{array}{l}{x′=5x}\\{{y}^{′}=4y}\end{array}\right.$ | B. | φ:$\left\{\begin{array}{l}{{x}^{′}=4x}\\{{y}^{′}=5y}\end{array}\right.$ | ||
| C. | φ:$\left\{\begin{array}{l}{{x}^{′}=\frac{1}{4}x}\\{{y}^{′}=\frac{1}{5}y}\end{array}\right.$ | D. | φ:$\left\{\begin{array}{l}{{x}^{′}=\frac{1}{5}x}\\{{y}^{′}=\frac{1}{4}y}\end{array}\right.$ |
分析 设$\left\{\begin{array}{l}{x′=λx}\\{y′=μy}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{x′}{λ}}\\{y=\frac{y′}{μ}}\end{array}\right.$,代入$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1后求得λ,μ值得答案.
解答 解:设$\left\{\begin{array}{l}{x′=λx}\\{y′=μy}\end{array}\right.$,则$\left\{\begin{array}{l}{x=\frac{x′}{λ}}\\{y=\frac{y′}{μ}}\end{array}\right.$,代入$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1得:
$\frac{(x′)^{2}}{16{λ}^{2}}+\frac{(y′)^{2}}{25{μ}^{2}}=1$,
∵椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1变换成单位圆,
∴16λ2=25μ2=1,即$λ=\frac{1}{4},μ=\frac{1}{5}$.
则φ:$\left\{\begin{array}{l}{x′=\frac{1}{4}x}\\{y′=\frac{1}{5}y}\end{array}\right.$.
故选:C.
点评 本题考查了伸缩变换,关键是对变换公式的理解与运用,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知i是虚数单位,a为实数,z为纯虚数,1+z=a+$\frac{1+i}{1-i}$,则z=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
7.已知集合A={x|x2=2},B={1,$\sqrt{2}$,2},则A∩B=( )
| A. | {$\sqrt{2}$} | B. | {2} | C. | {-$\sqrt{2}$,1,$\sqrt{2}$,2} | D. | {-2,1,$\sqrt{2}$,2} |
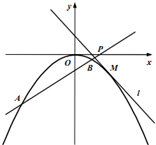 已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.
已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.