题目内容
20.在平面直角坐标系xOy中,圆C的参数方程为$\left\{\begin{array}{l}{x=1+cosφ}\\{y=sinφ}\end{array}\right.$ (φ为参数),以O为极点,x轴的非负半轴为为极轴建立极坐标系.(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程式2ρsin(θ+$\frac{π}{3}$ )=3$\sqrt{3}$,射线OM:θ=$\frac{π}{3}$与圆心C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
分析 (I)把cos2φ+sin2φ=1代入圆C的参数方程为$\left\{\begin{array}{l}{x=1+cosφ}\\{y=sinφ}\end{array}\right.$ (φ为参数),消去参数化为普通方程,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入可得圆C的极坐标方程.
(II)设P(ρ1,θ1),联立$\left\{\begin{array}{l}{ρ=2cosθ}\\{θ=\frac{π}{3}}\end{array}\right.$,解得ρ1,θ1;设Q(ρ2,θ2),联立$\left\{\begin{array}{l}{2ρ(sinθ+\sqrt{3}cosθ)=3\sqrt{3}}\\{θ=\frac{π}{3}}\end{array}\right.$,解得ρ2,θ2,可得|PQ|.
解答 解:(I)圆C的参数方程为$\left\{\begin{array}{l}{x=1+cosφ}\\{y=sinφ}\end{array}\right.$ (φ为参数),消去参数化为普通方程:(x-1)2+y2=1,
把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入可得圆C的极坐标方程:ρ=2cosθ.
(II)设P(ρ1,θ1),则$\left\{\begin{array}{l}{ρ=2cosθ}\\{θ=\frac{π}{3}}\end{array}\right.$,解得ρ1=1,θ1=$\frac{π}{3}$,
设Q(ρ2,θ2),则$\left\{\begin{array}{l}{2ρ(sinθ+\sqrt{3}cosθ)=3\sqrt{3}}\\{θ=\frac{π}{3}}\end{array}\right.$,解得ρ2=3,θ2=$\frac{π}{3}$,
∴|PQ|=2.
点评 本题考查了参数方程化为普通方程、直角坐标方程化为极坐标方程、弦长问题,考查了计算能力,属于中档题.

 53随堂测系列答案
53随堂测系列答案| A. | 1 | B. | -1 | C. | i | D. | -i |
| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{5}{2}$ |
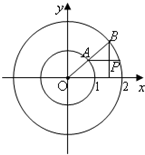 如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)
如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)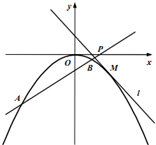 已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.
已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.