题目内容
1.设函数f(x)=lnx-ax(a∈R)(其中e=2.71828…).(Ⅰ)判断函数f(x)的单调性;
(Ⅱ)函数f(x)<0在(0,+∞)上恒成立时,求a的取值范围;
(Ⅲ)证明:当x∈(1,+∞)时,$\frac{x}{{{e^{x-1}}}}•{x^{\frac{1}{x-1}}}<e$.
分析 (Ⅰ)f′(x)=$\frac{1}{x}$-a,(x>0).对a分类讨论:a≤0,a>0,利用导数研究函数的单调性;
(Ⅱ)lnx-ax<0在(0,+∞)上恒成立?a>($\frac{lnx}{x}$)max,x∈(0,+∞).令f(x)=$\frac{lnx}{x}$,x∈(0,+∞).利用导数研究其单调性极值与最值即可得出;
(Ⅲ)把要证明的不等式$\frac{x}{{{e^{x-1}}}}•{x^{\frac{1}{x-1}}}<e$转化为lnx<x-1,构造函数g(x)=lnx-x+1,由导数加以证明.
解答 解:(Ⅰ)f′(x)=$\frac{1}{x}$-a,(x>0),
当a≤0时,f′(x)>0,函数f(x)在(0,+∞)单调递增;
当a>0时,f′(x)=$\frac{-a(x-\frac{1}{a})}{x}$,
令f′(x)>0,解得0<x<$\frac{1}{a}$;令f′(x)<0,解得x>$\frac{1}{a}$.
∴函数f(x)的单调递增区间为(0,$\frac{1}{a}$),单调递减区间为($\frac{1}{a}$,+∞).
综上可得:当a≤0时,函数f(x)在(0,+∞)单调递增;
当a>0时,函数f(x)的单调递增区间为(0,$\frac{1}{a}$),单调递减区间为($\frac{1}{a}$,+∞).
(Ⅱ)lnx-ax<0在(0,+∞)上恒成立?a>($\frac{lnx}{x}$)max,x∈(0,+∞).
令f(x)=$\frac{lnx}{x}$,x∈(0,+∞).
f′(x)=$\frac{1-lnx}{{x}^{2}}$,
当0<x<e时,f′(x)>0,此时函数f(x)单调递增;
当x>e时,f′(x)<0,此时函数f(x)单调递减.
∴当x=e时,函数f(x)取得最大值,f(e)=$\frac{1}{e}$.
∴a>$\frac{1}{e}$.
∴a的范围是($\frac{1}{e}$,+∞).
(Ⅲ)证明:当x∈(1,+∞)时,要证明$\frac{x}{{{e^{x-1}}}}•{x^{\frac{1}{x-1}}}<e$.
即证${x}^{\frac{1}{x-1}+1}$<ex,即证${x}^{\frac{x}{x-1}}$<ex,即证ln${x}^{\frac{x}{x-1}}$<lnex.
即证 $\frac{x}{x-1}$lnx<x,
∵x>1即证lnx<x-1,
令g(x)=lnx-x+1,
∵g′(x)=$\frac{1-x}{x}$<0,
∴g(x)在(1,+∞)上单调递减,
∴g(x)<g(1)=0,即lnx<x-1,
∴当x∈(1,+∞)时,$\frac{x}{{{e^{x-1}}}}•{x^{\frac{1}{x-1}}}<e$.
点评 本题考查导数的运用:求单调区间和极值、最值,同时考查不等式恒成立问题转化为求函数的最值问题,不等式的证明问题注意转化及运用已有结论,考查运算和推理能力,属于中档题.

| A. | x+2y-$\sqrt{3}$+$\frac{π}{3}$=0 | B. | x-2y+$\sqrt{3}$-$\frac{π}{3}$=0 | C. | $\sqrt{3}$x-2y+$\sqrt{3}$-$\frac{\sqrt{3}}{3}$π=0 | D. | $\sqrt{3}$x+2y-$\sqrt{3}$+$\frac{\sqrt{3}}{3}$π=0 |
| A. | 5760 | B. | 57600 | C. | 2880 | D. | 28800 |
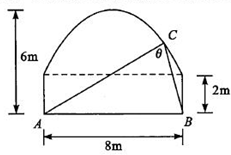 如图,一隧道截面由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )
如图,一隧道截面由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )| A. | 2$\sqrt{2}$m | B. | 2$\sqrt{3}$m | C. | 4m | D. | 6m |
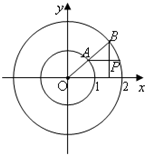 如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)
如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)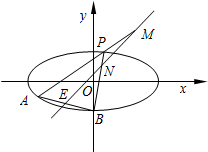 如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.
如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.