题目内容
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔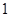 小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.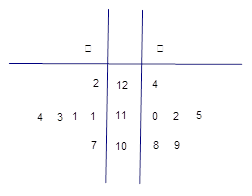
(1)根据样品数据,计算甲、乙两个车间产品重量的平均值与方差,并说明哪个车间的产品的重量相对较稳定;
(2)若从乙车间 件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过
件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过 克的概率.
克的概率.
(1)甲、乙两个车间产品重量的平均值都是 ,方差分别为
,方差分别为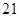 、
、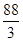 ,故甲车间的产品的重量相对较稳定;(2)所抽取的两件样品的重量之差不超过2克的概率为
,故甲车间的产品的重量相对较稳定;(2)所抽取的两件样品的重量之差不超过2克的概率为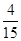 .
.
解析试题分析:(1)先从茎叶图中将甲、乙两个车间样品重量的数据记录下来,然后利用平均数公式与方差公式计算甲、乙两个车间产品重量的平均值与方差,利用平均数的大小与方差之间的大小来说明那个车间的产品重量相对稳定;(2)先将事件空间中的基本事件列举出来,并确定事件“所抽取的两件样品的重量之差不超过2克”所包含的基本事件,最后利用古典概型的概率计算公式计算该事件的概率.
试题解析:(1)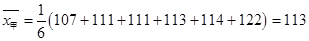 ,
, ,
,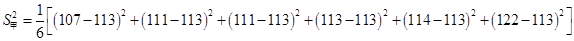
 ,
,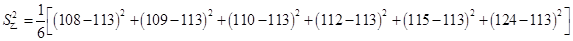
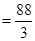 ,
,
∵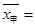
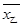 ,
,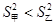 ,
,
∴甲车间的产品的重量相对较稳定.
(2)从乙车间6件样品中随机抽取两件,共有15种不同的取法: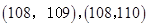
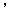
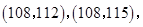
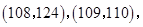
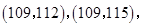
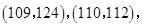
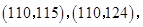
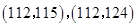 ,
,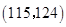 .
.
设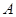 表示随机事件“所抽取的两件样品的重量之差不超过2克”,则
表示随机事件“所抽取的两件样品的重量之差不超过2克”,则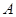 的基本事件有4种:
的基本事件有4种: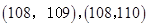 ,
,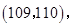
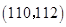 .
.
故所求概率为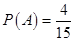 .
.
考点:1.平均数与方差;2.古典概型

 孟建平名校考卷系列答案
孟建平名校考卷系列答案为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
| 对别 | 北京 | 上海 | 天津 | 八一 |
| 人数 | 4 | 6 | 3 | 5 |
(Ⅱ)中国女排奋力拼搏,战胜了韩国队获得冠军,若要求选出两位队员代表发言,设其中来自北京队的人数为
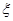 ,求随机变量
,求随机变量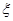 的分布列及数学期望
的分布列及数学期望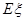
某食品企业一个月内被消费者投诉的次数用 表示,椐统计,随机变量
表示,椐统计,随机变量 的概率分布如下:
的概率分布如下:
 | 0 | 1 | 2 | 3 |
| p | 0.1 | 0.3 | 2a | a |
 的数学期望;
的数学期望;(2)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
为了比较“传统式教学法”与我校所创立的“三步式教学法”的教学效果.共选100名学生随机分成两个班,每班50名学生,其中一班采取“传统式教学法”,二班实行“三步式教学法”
(Ⅰ)若全校共有学生2000名,其中男生1100名,现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查,应抽取多少名女生?
(Ⅱ)下表1,2分别为实行“传统式教学”与“三步式教学”后的数学成绩:
表1
| 数学成绩 | 90分以下 | 90—120分 | 120—140分 | 140分以上 |
| 频 数 | 15 | 20 | 10 | 5 |
| 数学成绩 | 90分以下 | 90—120分 | 120—140分 | 140分以上 |
| 频 数 | 5 | 40 | 3 | 2 |
| 班 次 | 120分以下(人数) | 120分以上(人数) | 合计(人数) |
| 一班 | | | |
| 二班 | | | |
| 合计 | | | |
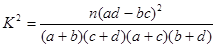 ,其中
,其中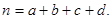
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 |
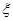 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
 分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足 的概率.
的概率.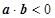 的概率.
的概率.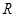 的函数:
的函数: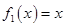 ,
, ,
,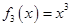 ,
,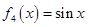 ,
,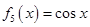 ,
,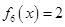 .
. 的分布列和数学期望.
的分布列和数学期望.