题目内容
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若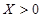 就去打球;若
就去打球;若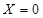 就去唱歌;若
就去唱歌;若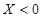 就去下棋.
就去下棋.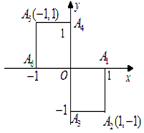
(Ⅰ)分别求小波去下棋的概率和不去唱歌的概率.
(Ⅱ)写出数量积X的所有可能取值,并求X分布列与数学期望
(Ⅰ)小波去下棋的概率为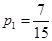 ,小波不去唱歌的概率
,小波不去唱歌的概率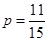 .(Ⅱ)
.(Ⅱ)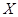 的所有可能取值为
的所有可能取值为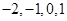 ;
;
解析试题分析:(Ⅰ) 在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目.已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表: 某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示: 的所有可能取值,即从
的所有可能取值,即从 ,
,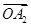 ,
,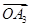 ,
, ,
, ,
,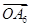 这六个向量中任取两个,共有
这六个向量中任取两个,共有 种,
种,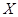 的所有可能取值为
的所有可能取值为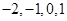 ,利用古典概型概率计算公式求解;(Ⅱ)由上表可知
,利用古典概型概率计算公式求解;(Ⅱ)由上表可知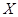 的所有可能取值为
的所有可能取值为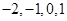 ;数量积为-2的只有一种,数量积为-1的有六种,数量积为0的有四种,数量积为1的有四种,列出分布列,求期望.
;数量积为-2的只有一种,数量积为-1的有六种,数量积为0的有四种,数量积为1的有四种,列出分布列,求期望.
试题解析:(Ⅰ)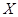 的所有可能取值,即从
的所有可能取值,即从 ,
,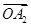 ,
,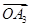 ,
, ,
, ,
,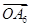 这六个向量中任取两个,共有
这六个向量中任取两个,共有 种。 1分
种。 1分
而对取出两个向量的数量积进行计算,得到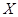 的所有可能取值为
的所有可能取值为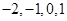 ; 3分
; 3分
求小波去下棋的概率,这显然是古典概型,只需找出总的事件数有 种,因为
种,因为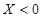 就去下棋,只需在下表计算结果中,找出小于零的次数为
就去下棋,只需在下表计算结果中,找出小于零的次数为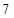 , 4分
, 4分
有古典概型的概率求法知:小波去下棋的概率为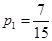 , 5分
, 5分
小波不去唱歌的概率,它的对立事件为,去唱歌,而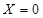 就去唱歌,
就去唱歌,
在下表中,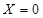 共有四次,故去唱歌的概率为
共有四次,故去唱歌的概率为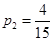 ,
,
由对立事件的概率求法知:小波不去唱歌的概率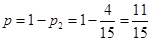 . 6分
. 6分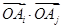

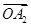
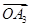



1 0 0 -1

帮你学数学全讲归纳精练系列答案
品至教育一线课堂系列答案
新优化设计暑假作业系列答案
三点一测课堂作业本系列答案
天梯学案初中同步新课堂系列答案
高考核心假期作业寒假中国原子能出版传媒有限公司系列答案
暑假作业湖南使用湖北教育出版社系列答案
常青藤英语词汇专练系列答案
新鑫文化过好假期每一天暑假团结出版社系列答案
精编名师点拨课时作业甘肃教育出版社系列答案
现从第一小组、第二小组中各任选2人分析选课情况.
科目甲
科目乙
总计
第一小组
1
5
6
第二小组
2
4
6
总计
3
9
12
(1)求选出的4人均选科目乙的概率;
(2)设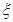 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求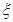 的分布列和数学期望.
的分布列和数学期望.
已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元.用付款方式 分1期 分2期 分3期 分4期 分5期 频数 40 20 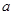
10 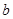
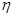 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.
(1)求上表中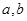 的值;
的值;
(2)若以频率作为概率,求事件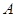 :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率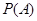 ;(3)求
;(3)求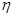 的分布列及数学期望
的分布列及数学期望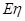 .
.
 ,各局比赛的结果相互独立,第1局甲当裁判.
,各局比赛的结果相互独立,第1局甲当裁判.
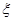 ,求随机变量
,求随机变量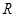 的函数:
的函数: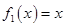 ,
, ,
,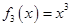 ,
,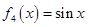 ,
,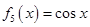 ,
,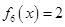 .
. 的分布列和数学期望.
的分布列和数学期望.