题目内容
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
 .
.(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为ξ,求ξ的分布列与期望.
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
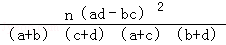 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
(1)
(2)在犯错误的概率不超过0.005的前提下,认为喜爱打篮球与性别有关. 喜爱打篮球 不喜爱打篮球 合计 男生 20 5 25 女生 10 15 25 合计 30 20 50
(3)ξ 0 1 2 P 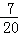

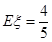
解析试题分析:(1)因为随机抽取1人抽到喜爱打篮球的学生的概率为 为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表: 某种产品按质量标准分为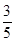 ,所以喜爱打篮球的学生人数为
,所以喜爱打篮球的学生人数为 ,则不喜爱打篮球的学生人数为
,则不喜爱打篮球的学生人数为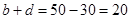 ,由表可得
,由表可得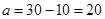 ,
,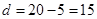 ,因此调查的人数中男生有
,因此调查的人数中男生有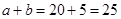 ,女生有
,女生有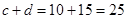 .
.
(2)由(1)得到的数据代入公式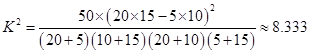 ,比对临界值表,因为
,比对临界值表,因为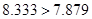 ,所以可以在犯错的概率不超过0.005的前提下,人为喜爱打篮球与性别无关.
,所以可以在犯错的概率不超过0.005的前提下,人为喜爱打篮球与性别无关.
(3)由(1)知调查的女生人数为25名,其中喜爱打篮球的女生人数为10名,从女生中抽取2名,则可以确定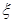 的值为0、1、2,根据古典概型计算公式得
的值为0、1、2,根据古典概型计算公式得 ,
, ,
,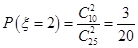 ,从而可列出所求
,从而可列出所求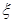 的分布列,再根据
的分布列,再根据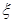 的分布列求出
的分布列求出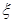 的期望
的期望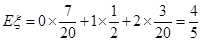 .
.
试题解析:(1)列联表补充如下: (3分)
(2)∵K2= 喜爱打篮球 不喜爱打篮球 合计 男生 20 5 25 女生 10 15 25 合计 30 20 50 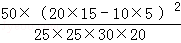 ≈8.333>7.879 (5分)
≈8.333>7.879 (5分)
∴在犯错误的概率不超过0.005的前提下,认为喜爱打篮球与性别有关. (6分)
(3)喜爱打篮球的女生人数ξ的可能取值为0,1,2. (7分)
其概率分别为P(ξ=0)= ,P(ξ=1)=
,P(ξ=1)=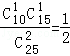 ,P(ξ=2)=
,P(ξ=2)=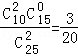 (10分)
(10分)
故ξ的分布列为:ξ 0 1 2 P 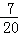


黄冈金牌之路妙解教材系列答案
黄冈金牌之路中考精英总复习系列答案
中考新夺标试题研究系列答案
汇测初中英语系列答案
会考结业学习手册系列答案
激活中考系列答案
加练半小时系列答案
尖子生超级训练系列答案
减负增效拓展三阶训练系列答案
江苏13大市中考28套卷系列答案
(Ⅰ)从这18名队员中随机选出两名,求两人来自同一队的概率;对别 北京 上海 天津 八一 人数 4 6 3 5
(Ⅱ)中国女排奋力拼搏,战胜了韩国队获得冠军,若要求选出两位队员代表发言,设其中来自北京队的人数为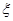 ,求随机变量
,求随机变量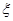 的分布列及数学期望
的分布列及数学期望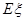
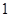 ,
, ,
,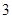 ,
,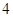 ,
,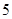 五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
(1)在抽取的20个产品中,等级为5的恰有2个,求等级 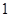

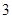
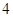
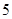
频率 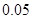
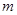
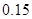
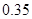
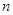
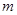 ,
, ;
;
(2)在(1)的条件下,从等级为3和5的所有产品中,任意抽取2个,求抽取的2个产品等级恰好相同的概率.
 名同学,现测得排球队
名同学,现测得排球队 )分别是:
)分别是: 、
、 、
、 、
、 、
、 、
、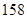 、
、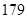 、
、 、
、 、
、 、
、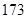 、
、 、
、 、
、 、
、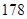 、
、
 ,求
,求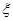 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求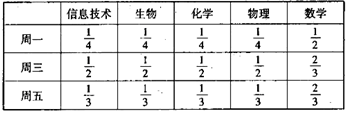
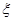 ,求随机变量
,求随机变量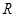 的函数:
的函数: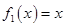 ,
, ,
,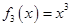 ,
,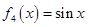 ,
,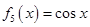 ,
,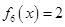 .
. 的分布列和数学期望.
的分布列和数学期望.