题目内容
【题目】已知数列{an}满足a1=1,|an+1﹣an|=pn , n∈N* .
(1)若{an}是递增数列,且a1 , 2a2 , 3a3成等差数列,求p的值;
(2)若p= ![]() ,且{a2n﹣1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式.
,且{a2n﹣1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式.
【答案】
(1)解:∵数列{an}是递增数列,∴an+1﹣an>0,
则|an+1﹣an|=pn化为:an+1﹣an=pn,
分别令n=1,2可得,a2﹣a1=p, ![]() ,
,
即a2=1+p, ![]() ,
,
∵a1,2a2,3a3成等差数列,∴4a2=a1+3a3,
即4(1+p)=1+3(p2+p+1),
化简得3p2﹣p=0,解得 ![]() 或0,
或0,
当p=0时,数列an为常数数列,不符合数列{an}是递增数列,
∴ ![]() ;
;
(2)解:由题意可得,|an+1﹣an|= ![]() ,
,
则|a2n﹣a2n﹣1|= ![]() ,|a2n+2﹣a2n+1|=
,|a2n+2﹣a2n+1|= ![]() ,
,
∵数列{a2n﹣1}是递增数列,且{a2n}是递减数列,
∴a2n+1﹣a2n﹣1>0,且a2n+2﹣a2n<0,
则﹣(a2n+2﹣a2n)>0,两不等式相加得
a2n+1﹣a2n﹣1﹣(a2n+2﹣a2n)>0,即a2n+1﹣a2n+2>a2n﹣1﹣a2n,
又∵|a2n﹣a2n﹣1|= ![]() >|a2n+2﹣a2n+1|=
>|a2n+2﹣a2n+1|= ![]() ,
,
∴a2n﹣a2n﹣1>0,即 ![]() ,
,
同理可得:a2n+3﹣a2n+2>a2n+1﹣a2n,即|a2n+3﹣a2n+2|<|a2n+1﹣a2n|,
则a2n+1﹣a2n= ![]()
当数列{an}的项数为偶数时,令n=2m(m∈N*),
![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
,
这2m﹣1个等式相加可得, ![]()
= 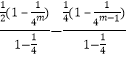 =
= ![]() ,
,
则 ![]() ;
;
当数列{an}的项数为奇数时,令n=2m+1(m∈N*)
![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
,
这2m个等式相加可得, ![]()
= 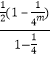 ﹣
﹣ 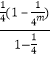 =
= ![]() ,
,
则 ![]() ,且当m=0时a1=1符合,
,且当m=0时a1=1符合,
故 ![]() ,
,
综上得, 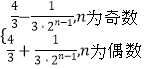
【解析】(1)根据条件去掉式子的绝对值,分别令n=1,2代入求出a2和a3 , 再由等差中项的性质列出关于p的方程求解,利用“{an}是递增数列”对求出的p的值取舍;(2)根据数列的单调性和式子“|an+1﹣an|=pn”、不等式的可加性,求出 ![]() 和a2n+1﹣a2n=
和a2n+1﹣a2n= ![]() ,再对数列{an}的项数分类讨论,利用累加法和等比数列前n项和公式,求出数列{an}的奇数项、偶数项对应的通项公式,再用分段函数的形式表示出来.
,再对数列{an}的项数分类讨论,利用累加法和等比数列前n项和公式,求出数列{an}的奇数项、偶数项对应的通项公式,再用分段函数的形式表示出来.
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系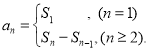 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

 阅读快车系列答案
阅读快车系列答案