题目内容
【题目】已知A(x1 , y1),B(x2 , y2)是函数f(x)= 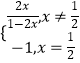 的图象上的任意两点(可以重合),点M在直线x=
的图象上的任意两点(可以重合),点M在直线x= ![]() 上,且
上,且 ![]() =
= ![]() .
.
(1)求x1+x2的值及y1+y2的值;
(2)已知S1=0,当n≥2时,Sn=f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() ),求Sn .
),求Sn .
【答案】
(1)解:∵点M在直线x= ![]() 上,设M
上,设M ![]() .
.
又 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴x1+x2=1.
①当x1= ![]() 时,x2=
时,x2= ![]() ,y1+y2=f(x1)+f(x2)=﹣1﹣1=﹣2;
,y1+y2=f(x1)+f(x2)=﹣1﹣1=﹣2;
②当x1≠ ![]() 时,x2≠
时,x2≠ ![]() .
.
y1+y2= ![]() +
+ ![]() =
= ![]() =
= ![]() =
= ![]() =﹣2.
=﹣2.
综合①②得,y1+y2=﹣2.
(2)解:由(1)知,当x1+x2=1.y1+y2=﹣2.
∴ ![]() +
+ ![]() =﹣2,k=1,2,3,…,n﹣1.)
=﹣2,k=1,2,3,…,n﹣1.)
n≥2时,Sn=f ![]() +f
+f ![]() +…+f
+…+f ![]() ,①
,①
∴Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,②
,②
①+②得,2Sn=﹣2(n﹣1),则Sn=1﹣n.
当n=1时,S1=0满足Sn=1﹣n.
∴Sn=1﹣n.
【解析】(1)点M在直线x= ![]() 上,设M
上,设M ![]() .又
.又 ![]() =
= ![]() ,利用坐标运算x1+x2=1.①当x1=
,利用坐标运算x1+x2=1.①当x1= ![]() 时,x2=
时,x2= ![]() ,y1+y2=f(x1)+f(x2);②当x1≠
,y1+y2=f(x1)+f(x2);②当x1≠ ![]() 时,x2≠
时,x2≠ ![]() .y1+y2=
.y1+y2= ![]() +
+ ![]() 化简即可得出.(2)由(1)知,当x1+x2=1.y1+y2=﹣2.可得
化简即可得出.(2)由(1)知,当x1+x2=1.y1+y2=﹣2.可得 ![]() +
+ ![]() =﹣2,k=1,2,3,…,n﹣1.即可得出.
=﹣2,k=1,2,3,…,n﹣1.即可得出.

练习册系列答案
相关题目