题目内容
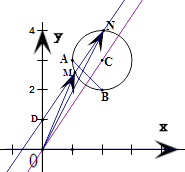
【题目】已知圆C经过点A（1，3）、B（2，2），并且直线m：3x﹣2y=0平分圆C．
（1）求圆C的方程；
（2）若过点D（0，1），且斜率为k的直线l与圆C有两个不同的交点M、N．
（Ⅰ）求实数k的取值范围；
（Ⅱ）若 
=12，求k的值．
【答案】
（1）解：设圆C的标准方程为（x﹣a）2+（y﹣b）2=r2
∵圆C被直线m：3x﹣2y=0平分，∴圆心C（a，b）在直线m上，可得3a﹣2b=0…①，
又∵点A（1，3）、B（2，2）在圆上，∴ 
…②，
将①②联解，得a=2，b=3，r=1．
∴圆C的方程是（x﹣2）2+（y﹣3）2=1
（2）解：过点D（0，1）且斜率为k的直线l方程为y=kx+1，即kx﹣y+1=0，
（I）∵直线l与圆C有两个不同的交点M、N，
∴点C（2，3）到直线l的距离小于半径r，
即 
，解之得 
＜k＜ 
；
（II）由 
消去y，得（1+k2）x2﹣（4+4k）x+7=0．
设直线l与圆C有两个不同的交点坐标分别为M（x1，y1）、N（x2，y2），
可得x1+x2= 
，x1x2= 
，
∴y1y2=（kx1+1）（kx2+1）=k2x1x2+k（x1+x2）+1= 
+ 
+1，
∵ 
= +（ + +1）=12，解之得k=1．
【解析】（1）设圆C的标准方程为（x﹣a）2+（y﹣b）2=r2 ． 由圆C被直线平分可得3a﹣2b=0，结合点A、B在圆上建立关于a、b、r的方程组，解出a、b、r的值即可得到圆C的方程；（2）（I）由题意，得直线l方程为kx﹣y+1=0，根据直线l与圆C有两个不同的交点，利用点到直线的距离建立关于k的不等式，解之即可得到实数k的取值范围；（II）直线l方程与圆C方程联解消去y，得（1+k2）x2﹣（4+4k）x+7=0．设M（x1 ， y1）、N（x2 ， y2），利用根与系数的关系、直线l方程和向量数量积的坐标运算公式，化简 =12得到关于k的方程，解之即可得到k的值．
【考点精析】通过灵活运用圆的标准方程，掌握圆的标准方程：
；圆心为A(a,b),半径为r的圆的方程即可以解答此题．
