题目内容
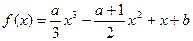
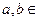
若曲线
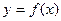 在点
在点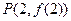 处的切线方程为
处的切线方程为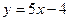 ,求函数
,求函数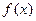 的解析式;
的解析式;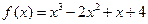
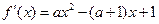 , ……………2分
, ……………2分由导数的几何意义得
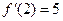 ,于是
,于是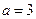 . ……….3分
. ……….3分由切点
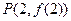 在直线
在直线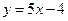 上可知
上可知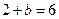 ,解得
,解得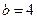 ……4分
……4分所以函数
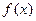 的解析式为
的解析式为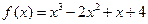 . .……5分
. .……5分
练习册系列答案
相关题目
题目内容
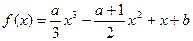
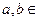
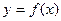 在点
在点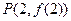 处的切线方程为
处的切线方程为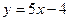 ,求函数
,求函数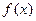 的解析式;
的解析式;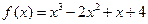
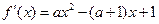 , ……………2分
, ……………2分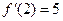 ,于是
,于是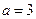 . ……….3分
. ……….3分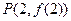 在直线
在直线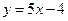 上可知
上可知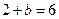 ,解得
,解得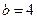 ……4分
……4分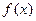 的解析式为
的解析式为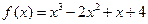 . .……5分
. .……5分