题目内容
设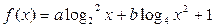 ,
,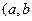 为常数).当
为常数).当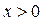 时,
时,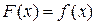 ,且
,且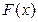 为
为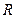 上的奇函数.
上的奇函数.
⑴ 若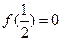 ,且
,且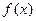 的最小值为
的最小值为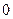 ,求
,求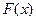 的表达式;
的表达式;
⑵ 在 ⑴ 的条件下,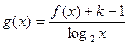 在
在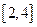 上是单调函数,求
上是单调函数,求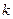 的取值范围.
的取值范围.
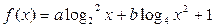 ,
,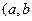 为常数).当
为常数).当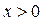 时,
时,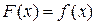 ,且
,且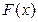 为
为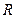 上的奇函数.
上的奇函数.⑴ 若
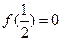 ,且
,且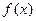 的最小值为
的最小值为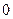 ,求
,求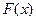 的表达式;
的表达式;⑵ 在 ⑴ 的条件下,
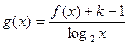 在
在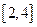 上是单调函数,求
上是单调函数,求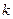 的取值范围.
的取值范围.(1)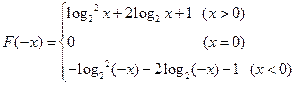
(2)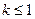 或
或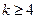
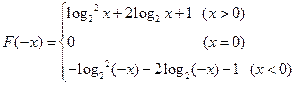
(2)
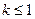 或
或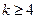
(1) 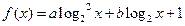 由
由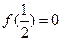 得
得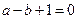 ,
,
∴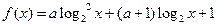
若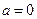 则
则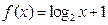 无最小值.∴
无最小值.∴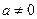 .
.
欲使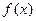 取最小值为0,只能使
取最小值为0,只能使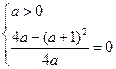 ,解得
,解得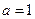 ,
,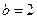 .
.
∴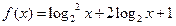
得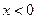 则
则 ,∴
,∴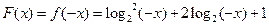
又 ,∴
,∴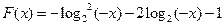
又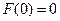 ∴
∴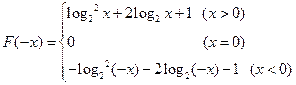
(2)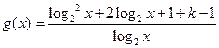
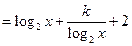 ,
,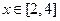 .
.
得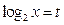 ,则
,则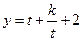 ,
,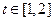 .
.
∴当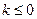 ,或
,或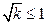 或
或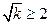 时,
时,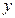 为单调函数.
为单调函数.
综上,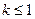 或
或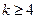 .
.
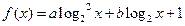 由
由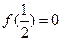 得
得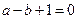 ,
, ∴
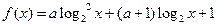
若
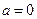 则
则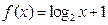 无最小值.∴
无最小值.∴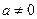 .
.欲使
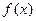 取最小值为0,只能使
取最小值为0,只能使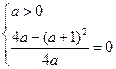 ,解得
,解得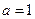 ,
,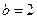 .
.∴
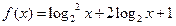
得
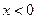 则
则 ,∴
,∴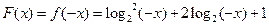
又
 ,∴
,∴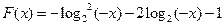
又
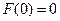 ∴
∴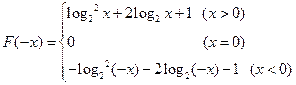
(2)
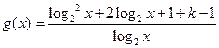
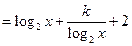 ,
,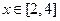 .
.得
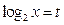 ,则
,则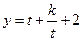 ,
,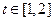 .
.∴当
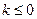 ,或
,或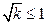 或
或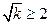 时,
时,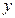 为单调函数.
为单调函数.综上,
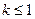 或
或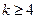 .
. 
练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
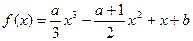
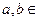
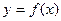 在点
在点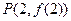 处的切线方程为
处的切线方程为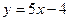 ,求函数
,求函数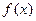 的解析式;
的解析式;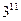 表示成
表示成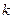 个连续正整数的和,求项数
个连续正整数的和,求项数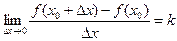 ,则
,则 等于( )
等于( )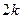
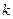

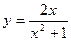 在点(1,1)处的切线方程;
在点(1,1)处的切线方程;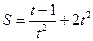 ,求t=3时的速度。
,求t=3时的速度。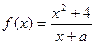 是奇函数。
是奇函数。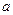 的值;
的值;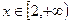 时,求
时,求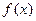 的反函数
的反函数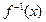 。
。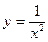 上两点
上两点 和
和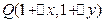 ,当
,当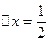 时,直线
时,直线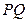 的斜率为( )
的斜率为( )
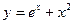 的图像上横坐标
的图像上横坐标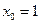 的点引切线,这条切线向上的方向与横轴的正向夹角的正切值是
的点引切线,这条切线向上的方向与横轴的正向夹角的正切值是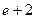 B.
B.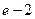 C.-2 D.2
C.-2 D.2