题目内容
【题目】对于给定的正整数![]() ,若数列
,若数列![]() 满足
满足![]() 对任意正整数
对任意正整数![]() 恒成立,则称数列
恒成立,则称数列![]() 是
是![]() 数列,若正数项数列
数列,若正数项数列![]() ,满足:
,满足:![]() 对任意正整数
对任意正整数![]() 恒成立,则称
恒成立,则称![]() 是
是![]() 数列;
数列;
(1)已知正数项数列![]() 是
是![]() 数列,且前五项分别为
数列,且前五项分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,求
,求![]() 的值;
的值;
(2)若![]() 为常数,且
为常数,且![]() 是
是![]() 数列,求
数列,求![]() 的最小值;
的最小值;
(3)对于下列两种情形,只要选作一种,满分分别是 ①![]() 分,②
分,②![]() 分,若选择了多于一种情形,则按照序号较小的解答记分.
分,若选择了多于一种情形,则按照序号较小的解答记分.
① 证明:数列![]() 是等差数列的充要条件为“
是等差数列的充要条件为“![]() 既是
既是![]() 数列,又是
数列,又是![]() 数列”;
数列”;
②证明:正数项数列![]() 是等比数列的充要条件为“数列
是等比数列的充要条件为“数列![]() 既是
既是![]() 数列,又是
数列,又是![]() 数列”.
数列”.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①证明见解析;②证明见解析.
;(3)①证明见解析;②证明见解析.
【解析】
(1)根据定义得出![]() ,再由
,再由![]() 可求出
可求出![]() 的值;
的值;
(2)根据定义得出![]() ,化简得出
,化简得出![]() ,然后利用两角和与差的正弦公式化简得出
,然后利用两角和与差的正弦公式化简得出![]() ,求出
,求出![]() 的值,由此可得出
的值,由此可得出![]() 的最小值;
的最小值;
(3)①利用等差中项的性质可推出充分性成立,由数列![]() 是
是![]() 数列和
数列和![]() 数列的定义推导出
数列的定义推导出![]() ,结合等差中项的定义可得知必要性成立;
,结合等差中项的定义可得知必要性成立;
②利用等比中项的定义可推出充分性成立,由数列![]() 是
是![]() 数列和
数列和![]() 数列的定义推导出
数列的定义推导出![]() ,利用等比中项的定义可得知必要性成立.
,利用等比中项的定义可得知必要性成立.
(1)由于正项数列![]() 是
是![]() 数列,则
数列,则![]() ,
,![]() ,解得
,解得![]() ;
;
(2)由于数列![]() 是
是![]() 数列,对任意的
数列,对任意的![]() ,
,![]() ,
,
则有![]() ,
,
化简得![]() ,
,
由两角和与差的正弦公式可得![]() ,
,
上述等式对任意的![]() 的正整数
的正整数![]() 恒成立,所以,
恒成立,所以,![]() ,
,
即![]() ,
,![]() ,解得
,解得![]() ,
,![]() 正数
正数![]() 的最小值为
的最小值为![]() ;
;
(3)①充分性:若数列![]() 是等差数列,当
是等差数列,当![]() 时,由等差中项的性质可得
时,由等差中项的性质可得![]() ,
,![]() ,
,![]() ,
,
上述等式全部相加得![]() ,
,
![]() ,则数列
,则数列![]() 是
是![]() 数列.
数列.
当![]() 时,由等差中项的性质可得
时,由等差中项的性质可得![]() ,
,![]() ,
,
上述等式全部相加得![]() ,
,![]() ,
,
则数列![]() 是
是![]() 数列.
数列.
必要性:若数列![]() 是
是![]() 数列,当
数列,当![]() 时,
时,
则![]() ,(i)
,(i)
若数列![]() 是
是![]() 数列,则
数列,则![]() ,(ii)
,(ii)
![]() ,(iii)
,(iii)
(iii)![]() (ii)
(ii)![]() (i)得,
(i)得,![]() ,化简得
,化简得![]() .
.
因此,当![]() 时,数列
时,数列![]() 从第三项开始成等差数列,设公差为
从第三项开始成等差数列,设公差为![]() .
.
注意到![]() ,
,
可得![]() ,
,
因为![]() ,
,
可得![]() ,
,
即数列![]() 前
前![]() 项也满足等差数列的通项公式,所以,数列
项也满足等差数列的通项公式,所以,数列![]() 是等差数列.
是等差数列.
因此,数列![]() 是等差数列的充要条件为“
是等差数列的充要条件为“![]() 既是
既是![]() 数列,又是
数列,又是![]() 数列”;
数列”;
②充分性:若数列![]() 是等比数列,当
是等比数列,当![]() 时,由等比中项的性质可得
时,由等比中项的性质可得![]() ,
,![]() ,
,![]() ,上述等式全部相乘得
,上述等式全部相乘得![]() ,
,
所以,![]() ,则等比数列
,则等比数列![]() 为
为![]() 数列;
数列;
若数列![]() 是等比数列,当
是等比数列,当![]() 时,由等比中项的性质可得,
时,由等比中项的性质可得,![]() ,
,![]() ,上述等式全部相乘得
,上述等式全部相乘得![]() ,所以,
,所以,![]() ,
,
则等比数列![]() 为
为![]() 数列;
数列;
必要性:若数列![]() 是
是![]() 数列,当
数列,当![]() 时,则
时,则![]() ,(iv)
,(iv)
若数列![]() 是
是![]() 数列,则
数列,则![]() ,(v)
,(v)![]() ,(vi)
,(vi)
(iv)![]() (v)
(v)![]() (vi)得,
(vi)得,![]() ,
,![]() ,化简得
,化简得![]() .
.
因此,当![]() 时,数列
时,数列![]() 从第三项开始成等比数列,设公比为
从第三项开始成等比数列,设公比为![]() .
.
注意到![]() ,可得
,可得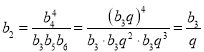 ,
,
因为![]() ,
,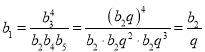 ,
,
即数列![]() 前
前![]() 项也满足等比数列的通项公式,所以,数列
项也满足等比数列的通项公式,所以,数列![]() 是等比数列.
是等比数列.
因此,正数项数列![]() 是等比数列的充要条件为“数列
是等比数列的充要条件为“数列![]() 既是
既是![]() 数列,又是
数列,又是![]() 数列”.
数列”.