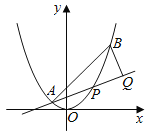
题目内容
【题目】对于定义在![]() 上的函数
上的函数![]() ,如果存在两条平行直线
,如果存在两条平行直线![]() 与
与![]()
![]() ,使得对于任意
,使得对于任意![]() ,都有
,都有![]() 恒成立,那么称函数
恒成立,那么称函数![]() 是带状函数,若
是带状函数,若![]() ,
,![]() 之间的最小距离
之间的最小距离![]() 存在,则称
存在,则称![]() 为带宽.
为带宽.
(1)判断函数![]() 是不是带状函数?如果是,指出带宽(不用证明);如果不是,说明理由;
是不是带状函数?如果是,指出带宽(不用证明);如果不是,说明理由;
(2)求证:函数![]() (
(![]() )是带状函数;
)是带状函数;
(3)求证:函数![]() (
(![]() )为带状函数的充要条件是
)为带状函数的充要条件是![]() .
.
【答案】(1)是,带宽![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
(1)先理解带状函数的特征,再求函数的值域即可得解;
(2)由函数![]() ,(
,(![]() )的图像表示双曲线
)的图像表示双曲线![]() 在第一象限的部分,
在第一象限的部分,
再结合双曲线的渐近线即可找出两平行直线;
(3)由分段函数的图像特征,结合带状函数的定义,分别证明充分性及必要性即可.
解:(1)因为![]() ,所以
,所以![]() ,
,
取直线![]() ,则
,则![]() 恒成立,
恒成立,
即函数![]() 是带状函数,带宽为
是带状函数,带宽为![]() ;
;
(2)因为![]() ,(
,(![]() )表示双曲线
)表示双曲线![]() 在第一象限的部分,又双曲线的渐近线方程为
在第一象限的部分,又双曲线的渐近线方程为![]() ,故函数
,故函数![]() 满足
满足![]() ,则函数
,则函数![]() 为
为![]() 有一个宽带为
有一个宽带为![]() 的带状函数;
的带状函数;
(3)函数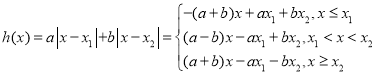 ,
,
先证充分性,当![]() 时,
时,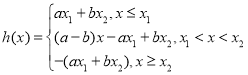 ,
,
不妨设![]() ,则
,则![]() ,即存在直线
,即存在直线![]() ,
,![]() ,满足题意,即函数
,满足题意,即函数![]() 为带状函数,
为带状函数,
再证必要性,当函数![]() (
(![]() )为带状函数,
)为带状函数,
则存在![]() ,又
,又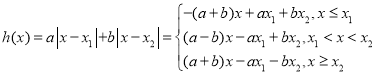 ,当
,当![]() ,则直线
,则直线![]() 与两直线
与两直线![]() ,
,![]() 中至少一条相交,故不满足
中至少一条相交,故不满足![]() ,即
,即![]() 不满足题意,即
不满足题意,即![]() ,
,
故函数![]() (
(![]() )为带状函数的充要条件是
)为带状函数的充要条件是![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目