题目内容
【题目】如图1,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,D,E分别是AC,AB上的点,
,D,E分别是AC,AB上的点,![]() ,将
,将![]() 沿DE折起,得到如图2所示的四棱锥
沿DE折起,得到如图2所示的四棱锥![]() ,使得
,使得![]() .
.
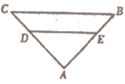
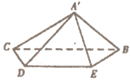
图1 图2
(1)证明:平面![]() 平面BCD;
平面BCD;
(2)求![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)证明见解析
(2)![]()
【解析】
(1)取BC中点O,连接OD,OE,因为![]() ,O为BC中点,根据题意即可求出
,O为BC中点,根据题意即可求出![]() ,
,![]() ,由
,由![]() 即可得到
即可得到![]() ,即可说明
,即可说明![]() 平面BCD,则可证明平面
平面BCD,则可证明平面![]() 平面BCD.
平面BCD.
(2)以O点为原点,建立空间直角坐标系O-xyz. 则可写出![]() ,
,![]() ,
,![]() ,
,![]() 的坐标,即可求出平面
的坐标,即可求出平面![]() 的法向量
的法向量![]() ,利用公式
,利用公式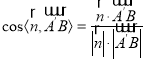 ,即可求出答案.
,即可求出答案.
(1)如图所示:
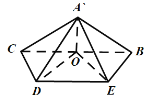
取BC中点O,连接OD,OE,因为![]() ,O为BC中点,
,O为BC中点,
所以![]()
则![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
在![]() 中,
中,![]() ,所以
,所以![]() .
.
∵![]() ,∴
,∴![]() 平面BCD.
平面BCD.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面BCD.
平面BCD.
(2)如图所示:
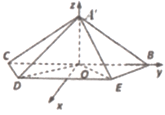
以O点为原点,建立空间直角坐标系O-xyz,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则
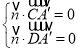 ,即
,即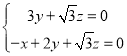 ,令
,令![]() ,得
,得![]() .
.
又![]() ,
,
所以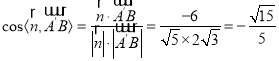 .
.
即![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
所以![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为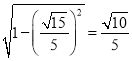

练习册系列答案
相关题目
【题目】某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种