题目内容
设函数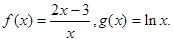
(1)试判断当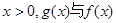 的大小关系;
的大小关系;
(2)求证: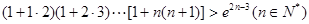 ;
;
(3)设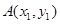 、
、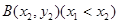 是函数
是函数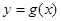 的图象上的两点,且
的图象上的两点,且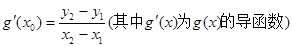 ,证明:
,证明: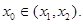
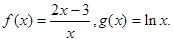
(1)试判断当
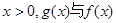 的大小关系;
的大小关系;(2)求证:
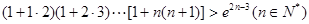 ;
;(3)设
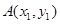 、
、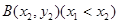 是函数
是函数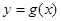 的图象上的两点,且
的图象上的两点,且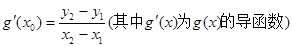 ,证明:
,证明: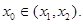
(1) (2)见解析 (3)证明见解析
(2)见解析 (3)证明见解析
 (2)见解析 (3)证明见解析
(2)见解析 (3)证明见解析(1)设F(x)=g(x)-f(x),(x>0),
然后求导,利用导数求出F(x)的最小值,说明最小值大于0即可.
(2)证明:由(1)知 ,
,
令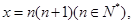 则
则
然后再利用不等式的性质同向不等式具有可加性进行证明即可
(1)设 则
则 由
由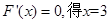

 时,
时,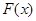 取得最小值为
取得最小值为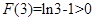
 即
即 …………5分
…………5分
(2)证明:由(1)知
令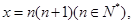 则
则 ……7分
……7分

 …………10分
…………10分
(3)证明: ,于是
,于是 ,
,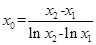 ,
,
以下证明 等价于
等价于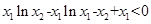 .令
.令 …………12分则
…………12分则 ,在
,在 上,
上, 
所以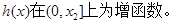 当
当 即
即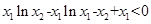 从而
从而 ,得到证明.对于
,得到证明.对于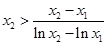 同理可证.
同理可证.
所以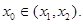 …………16分
…………16分
另法:(3)证明:
 ,于是
,于是 ,
,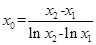 ,
,
以下证明 .只要证:
.只要证: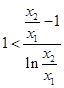 ,即证:
,即证:
设: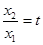 ,
, …………12分
…………12分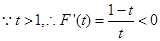 ,
,
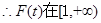 上为减函数,
上为减函数, ,
,
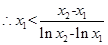 ,即
,即 .同理可证:
.同理可证: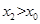 所以
所以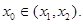
然后求导,利用导数求出F(x)的最小值,说明最小值大于0即可.
(2)证明:由(1)知
 ,
,令
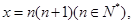 则
则
然后再利用不等式的性质同向不等式具有可加性进行证明即可
(1)设
 则
则 由
由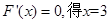

 时,
时,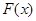 取得最小值为
取得最小值为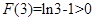
 即
即 …………5分
…………5分(2)证明:由(1)知

令
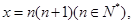 则
则 ……7分
……7分
 …………10分
…………10分(3)证明:
 ,于是
,于是 ,
,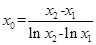 ,
,以下证明
 等价于
等价于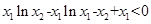 .令
.令 …………12分则
…………12分则 ,在
,在 上,
上, 
所以
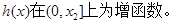 当
当 即
即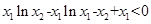 从而
从而 ,得到证明.对于
,得到证明.对于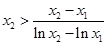 同理可证.
同理可证.所以
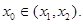 …………16分
…………16分另法:(3)证明:

 ,于是
,于是 ,
,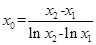 ,
,以下证明
 .只要证:
.只要证: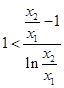 ,即证:
,即证:
设:
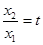 ,
, …………12分
…………12分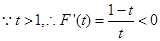 ,
,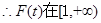 上为减函数,
上为减函数, ,
,
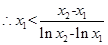 ,即
,即 .同理可证:
.同理可证: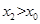 所以
所以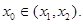

练习册系列答案
相关题目
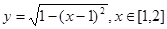 对于满足
对于满足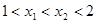 的任意
的任意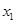 ,
,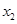 ,给出下列结论:
,给出下列结论: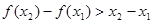 ; ②
; ②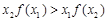 ;
;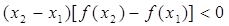 . ④
. ④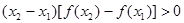
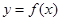 的反函数为
的反函数为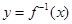 ,定义:若对给定的实数
,定义:若对给定的实数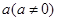 ,函数
,函数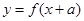 与
与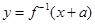 互为反函数,则称
互为反函数,则称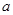 和性质”.
和性质”.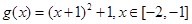 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;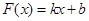 ,其中
,其中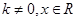 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得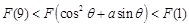 对任意的
对任意的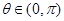 恒成立?若存在,求出
恒成立?若存在,求出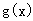 是
是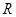 上的奇函数,且当
上的奇函数,且当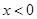 时
时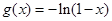 ,
,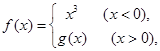 若
若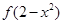 >
>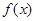 ,则实数
,则实数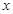 的取值范围是
的取值范围是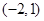
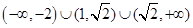
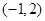
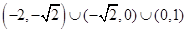
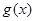 是定义在
是定义在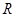 上、以2为周期的函数,若
上、以2为周期的函数,若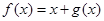 在
在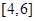 上的值域为
上的值域为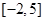 ,则
,则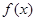 在区间
在区间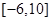 上的值域为 .
上的值域为 .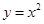
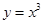
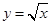
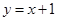
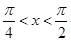 ,则函数
,则函数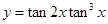 的最大值为 .
的最大值为 .