题目内容
6.已知△ABC的三边长分别为AB=$\sqrt{{m}^{2}+{n}^{2}}$,AC=$\sqrt{{m}^{2}+{t}^{2}}$,BC=$\sqrt{{n}^{2}+{t}^{2}}$,其中m,n,t∈(0,+∞),则△ABC是( )| A. | 直角三角形 | B. | 钝角三角形 | ||
| C. | 锐角三角形 | D. | 以上三种情况都有可能 |
分析 利用余弦定理,确定A,B,C是锐角,即可得出结论.
解答 解:∵△ABC的三边长分别为AB=$\sqrt{{m}^{2}+{n}^{2}}$,AC=$\sqrt{{m}^{2}+{t}^{2}}$,BC=$\sqrt{{n}^{2}+{t}^{2}}$,
∴AB2+AC2-BC2=2m2>0,AB2+BC2-AC2=2n2>0,AC2+BC2-AB2=2t2>0,
∴cosA>0,cosB>0,cosC>0,
∴A,B,C是锐角,
∴△ABC是锐角三角形,
故选:C.
点评 本题考查余弦定理的运用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
8.已知中心在原点,焦点在坐标轴上的双曲线与圆x2+y2=17有公共点A(1,-4),且圆在A点的切线与双曲线的渐近线平行,则双曲线的离心率为( )
| A. | $\frac{\sqrt{17}}{4}$ | B. | $\sqrt{17}$ | C. | $\frac{\sqrt{17}}{4}$或$\sqrt{17}$ | D. | 以上都不对 |
9.若m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中正确的是( )
| A. | α∥β,m?α,n?β⇒m∥n | B. | α⊥β,n∥α,m⊥β⇒n⊥m | C. | m∥n,m∥α⇒n∥α | D. | m∥n,m⊥α⇒n⊥α |
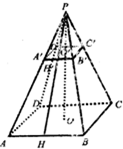 如图所示,正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截,得到正四棱台OO′和较小的棱锥PO′,其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$,侧棱PA长为15cm,小棱锥底面边长A′B′为6cm.
如图所示,正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截,得到正四棱台OO′和较小的棱锥PO′,其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$,侧棱PA长为15cm,小棱锥底面边长A′B′为6cm.