题目内容
18.已知$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-2,4),$\overrightarrow{c}$=(-1,-2),求$\overrightarrow{a}$•$\overrightarrow{b}$,($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$),$\overrightarrow{a}$•($\overrightarrow{b}$+$\overrightarrow{c}$),($\overrightarrow{a}$+$\overrightarrow{b}$)2.分析 利用向量坐标运算性质、模的计算公式即可得出.
解答 解:$|\overrightarrow{a}|$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,$|\overrightarrow{b}|$=$\sqrt{(-2)^{2}+{4}^{2}}$=2$\sqrt{5}$.
$\overrightarrow{a}$•$\overrightarrow{b}$=2×(-2)+3×4=8,
($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}$=13-20=-7,
$\overrightarrow{a}$•($\overrightarrow{b}$+$\overrightarrow{c}$)=(2,3)•(-3,2)=-6+6=0.
∵$\overrightarrow{a}+\overrightarrow{b}$=(0,7),
∴($\overrightarrow{a}$+$\overrightarrow{b}$)2=72=49.
点评 本题考查了向量数量积运算性质、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
6.已知△ABC的三边长分别为AB=$\sqrt{{m}^{2}+{n}^{2}}$,AC=$\sqrt{{m}^{2}+{t}^{2}}$,BC=$\sqrt{{n}^{2}+{t}^{2}}$,其中m,n,t∈(0,+∞),则△ABC是( )
| A. | 直角三角形 | B. | 钝角三角形 | ||
| C. | 锐角三角形 | D. | 以上三种情况都有可能 |
3.下列表述正确的是( )
①归纳推理是由部分到整体的推理;
②归纳推理是由一般到一般的推理;
③演绎推理是由一般到特殊的推理;
④类比推理是由特殊到一般的推理;
⑤类比推理是由特殊到特殊的推理.
①归纳推理是由部分到整体的推理;
②归纳推理是由一般到一般的推理;
③演绎推理是由一般到特殊的推理;
④类比推理是由特殊到一般的推理;
⑤类比推理是由特殊到特殊的推理.
| A. | ①②③ | B. | ②③④ | C. | ①③⑤ | D. | ②④⑤ |
20.某程序框图如图所示,则输出的结果为( )
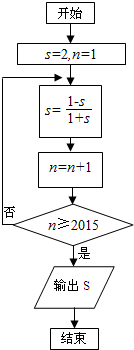

| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{3}$ | D. | -3 |