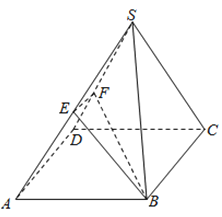
题目内容
【题目】已知点![]() 是椭圆
是椭圆![]() 的右焦点,过点
的右焦点,过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,当直线
两点,当直线![]() 过
过![]() 的下顶点时,
的下顶点时,![]() 的斜率为
的斜率为![]() ,当直线
,当直线![]() 垂直于
垂直于![]() 的长轴时,
的长轴时,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅲ)若直线![]() 上存在点
上存在点![]() 满足
满足![]() 成等比数列,且点
成等比数列,且点![]() 在椭圆外,证明:点
在椭圆外,证明:点![]() 在定直线上.
在定直线上.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
(Ⅰ)根据题意得:![]() ,
,![]() ,及
,及![]() ,解得
,解得![]() ,进而可得椭圆的方程;
,进而可得椭圆的方程;
(Ⅱ)分两种情况:当直线![]() 与
与![]() 轴重合时,得
轴重合时,得![]() ,不合题意;当直线
,不合题意;当直线![]() 与
与![]() 轴不重合时,设直线
轴不重合时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,联立直线与椭圆得方程,结合根与系数关系得
,联立直线与椭圆得方程,结合根与系数关系得![]() ,由
,由![]() ,得
,得![]() ,组成方程组解得
,组成方程组解得![]() ,进而可得直线
,进而可得直线![]() 的方程;
的方程;
(Ⅲ)设![]() ,分两种情况讨论,当直线
,分两种情况讨论,当直线![]() 与
与![]() 轴重合时,当直线
轴重合时,当直线![]() 与
与![]() 轴不重合时,由
轴不重合时,由![]() ,解得
,解得![]() ,所以点
,所以点![]() 在定直线
在定直线![]() 上.
上.
解:(Ⅰ)由题设:![]() ,
,![]() ,
,
解得:![]() ,
,
所以椭圆![]() 的方程为:
的方程为:![]() .
.
(Ⅱ)当直线![]() 与
与![]() 轴重合时,可得
轴重合时,可得![]() ,不合题意;
,不合题意;
当直线![]() 与
与![]() 轴不重合时,设直线
轴不重合时,设直线![]() 的方程为:
的方程为:![]() ,
,
设![]() ,联立
,联立![]() ,
,
消去![]() 整理得:
整理得:![]() ,
,
有![]() ①,
①,![]() ②,
②,
由![]() ,得
,得![]() ③,
③,
联立①②③得![]() ,
,
解得:![]() ,
,
所以直线![]() 的方程为:
的方程为:![]() .
.
(Ⅲ)设![]() ,
,
当直线![]() 与
与![]() 轴重合时,因为点
轴重合时,因为点![]() 在椭圆外,所以
在椭圆外,所以![]() 同号,
同号,
由![]() ,
,
得![]() ,解得:
,解得:![]() ,
,
当直线![]() 与
与![]() 轴不重合时,
轴不重合时,
由(Ⅱ)知![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
因为点![]() 在椭圆外,所以
在椭圆外,所以![]() 同号,
同号,
由![]() ,
,
得![]() ,
,
整理得:![]() ,
,
即![]() ,
,
解得:![]() ,
,
代入直线![]() 方程
方程![]() ,得:
,得:![]() ,
,
所以点![]() 在定直线
在定直线![]() 上.
上.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】自从新型冠状病毒爆发以来,全国范围内采取了积极的措施进行防控,并及时通报各项数据以便公众了解情况,做好防护.以下是湖南省2020年1月23日-31日这9天的新增确诊人数.
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
时间 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
新增确诊人数 | 15 | 19 | 26 | 31 | 43 | 78 | 56 | 55 | 57 |
经过医学研究,发现新型冠状病毒极易传染,一个病毒的携带者在病情发作之前通常有长达14天的潜伏期,这个期间如果不采取防护措施,则感染者与一位健康者接触时间超过15秒,就有可能传染病毒.
(1)将1月23日作为第1天,连续9天的时间作为变量x,每天新增确诊人数作为变量y,通过回归分析,得到模型![]() 用于对疫情进行分析.对上表的数据作初步处理,得到下面的一些统计量的值(部分数据已作近似处理):
用于对疫情进行分析.对上表的数据作初步处理,得到下面的一些统计量的值(部分数据已作近似处理):![]() ,
,![]() .根据相关数据,求该模型的回归方程(结果精确到0.1),并依据该模型预测第10天新增确诊人数.
.根据相关数据,求该模型的回归方程(结果精确到0.1),并依据该模型预测第10天新增确诊人数.
(2)如果一位新型冠状病毒的感染者传染给他人的概率为0.3,在一次12人的家庭聚餐中,只有一位感染者参加了聚餐,记余下的人员中被感染的人数为![]() ,求
,求![]() 最有可能(即概率最大)的值是多少.
最有可能(即概率最大)的值是多少.
附:对于一组数据![]() ,
,![]() …,
…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为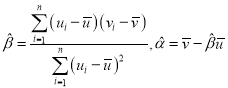 .
.