题目内容
【题目】如图,正四棱锥![]() 的底面边长为
的底面边长为![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
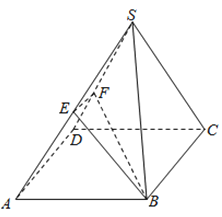
(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 与底面
与底面![]() 所成锐二面角为
所成锐二面角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据四棱锥是正四棱锥,连接![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为原点,以
为原点,以![]() 、
、![]() 、
、![]() 建立空间坐标系.取
建立空间坐标系.取![]() 的中点
的中点![]() ,用向量法证明
,用向量法证明![]() ,
,![]() ,得到
,得到![]() 平面
平面![]() ,再用面面垂直的判定定理证明;
,再用面面垂直的判定定理证明;
(2)设![]() ,求得平面
,求得平面![]() 的一个法向量,取平面
的一个法向量,取平面![]() 的一个法向量,根据平面
的一个法向量,根据平面![]() 与底面
与底面![]() 所成锐二面角为
所成锐二面角为![]() ,由
,由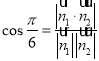 ,求得
,求得![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,代入公式
,代入公式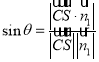 求解.
求解.
(1)连接![]() 交
交![]() 于点
于点![]() ,建立如图所示空间坐标系.
,建立如图所示空间坐标系.
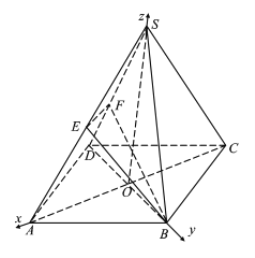
∵![]() ,∴
,∴![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,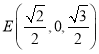 ,
,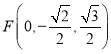 ,
,
设![]() 是
是![]() 的中点,则
的中点,则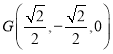 ,
,
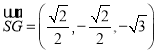 ,
,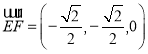 ,
,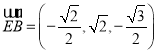 ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)设![]() ,则
,则![]() ,
,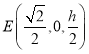 ,
,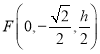 ,
,
则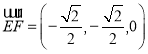 ,
,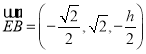 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则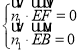 ,即
,即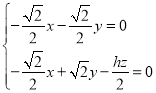 ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以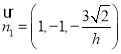 ,
,
取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则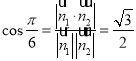 ,即
,即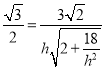 ,解得
,解得![]() ,∴
,∴![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,∴
,∴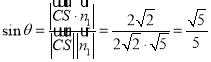 ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】“未来肯定是非接触的,无感支付的方式将成为主流,这有助于降低交互门槛”.云从科技联合创始人姚志强告诉南方日报记者.相对于主流支付方式二维码支付,刷脸支付更加便利,以前出门一部手机解决所有,而现在连手机都不需要了,毕竟,手机支付还需要携带手机,打开二维码也需要时间和手机信号.刷脸支付将会替代手机,成为新的支付方式.某地从大型超市门口随机抽取50名顾客进行了调查,得到了如下列联表:
男性 | 女性 | 总计 | |
刷脸支付 | 18 | 25 | |
非刷脸支付 | 13 | ||
总计 | 50 |
(1)请将上面的列联表补充完整,并判断是否有95%的把握认为使用刷脸支付与性别有关?
(2)从参加调查且使用刷脸支付的顾客中随机抽取2人参加抽奖活动,抽奖活动规则如下:
“一等奖”中奖概率为0.25,奖品为10元购物券![]() 张(
张(![]() ,且
,且![]() ),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为
),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为![]() 元,若要使
元,若要使![]() 的均值不低于50元,求
的均值不低于50元,求![]() 的最小值.
的最小值.
附: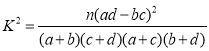 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.869 |