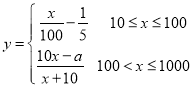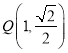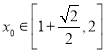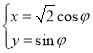题目内容
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且函数
,且函数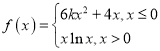 ,若方程
,若方程![]() 至少有三个实数根,则实数
至少有三个实数根,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由等比数列前![]() 项和的性质,求得参数
项和的性质,求得参数![]() ,再将方程根的个数的问题,转化为函数图像交点个数的问题,利用导数求得直线与函数相切时的斜率,即可求得参数的范围.
,再将方程根的个数的问题,转化为函数图像交点个数的问题,利用导数求得直线与函数相切时的斜率,即可求得参数的范围.
因为等比数列![]() 的前
的前![]() 项和为
项和为![]()
根据等比数列前![]() 项和的性质,容易知
项和的性质,容易知![]() ,解得
,解得![]() .
.
令![]() ,则
,则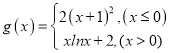
方程![]() 至少有三个实数根
至少有三个实数根
等价于![]() 至少有三个实数根,
至少有三个实数根,
也等价于函数![]() 与直线
与直线![]() 有至少三个交点,
有至少三个交点,
又![]() 是斜率为
是斜率为![]() ,且恒过
,且恒过![]() 的直线,
的直线,
故只需求出函数![]() 与直线有三个交点的临界状态时,对应直线的斜率即可.
与直线有三个交点的临界状态时,对应直线的斜率即可.
则在同一直角坐标系下画出函数图像如下所示:
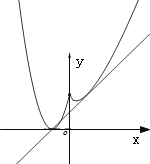
由图可知,当直线与![]() 相切时,恰有三个交点,
相切时,恰有三个交点,
设切点为![]() ,
,![]() ,故过切点的切线方程为:
,故过切点的切线方程为:
![]() ,又因为
,又因为![]() ,且该切线过点
,且该切线过点![]()
故可得![]()
即![]() ,解得
,解得![]() ,
,
故切点为![]() ,此时直线的斜率为
,此时直线的斜率为![]()
此时有三个交点,故![]() 可取;
可取;
又根据图象可知,当直线过点![]() 时,也是临界状态,
时,也是临界状态,
此时直线的斜率为![]()
此时有三个交点,故![]() 可取;
可取;
综上所述,要满足题意,只需![]() 即可.
即可.
故选:C.

练习册系列答案
相关题目