题目内容
【题目】如图,三棱柱![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
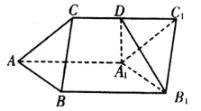
(1)求证:![]() ;
;
(2)若![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() 为
为![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)过点C作CO⊥AA1,则CO⊥平面AA1B1B,CO⊥OB,推导出Rt△AOC≌Rt△BOC,从而AA1⊥OB,再由AA1⊥CO,得AA1⊥平面BOC,由此能证明AA1⊥BC.
(2)以O为坐标原点,OA,OB,OC所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角B1﹣A1D﹣C1的余弦值.
(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
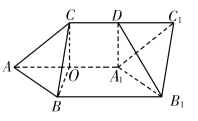
因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() ,
,
又因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,故
,故![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() .
.
(2)以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
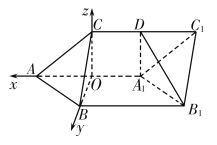
因为![]() 平面
平面![]() ,
,
所以![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,
所成角,
故![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
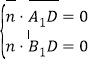 ,所以
,所以![]() ,
,
令![]() ,得
,得![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() 为平面
为平面![]() 的一条法向量,
的一条法向量,
![]() ,
,
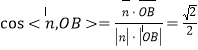 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某公司为了解用户对其产品的满意度,从A、B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
B地区: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度的平均值及分散程度(不要求算出具体值,给出结论即可):

(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率。