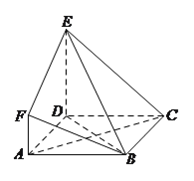
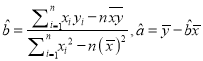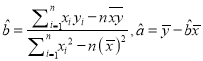题目内容
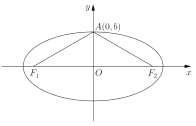
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,设点
,设点![]() ,在
,在![]() 中,
中, ![]() ,周长为
,周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 与
与![]() 的斜率之和为
的斜率之和为![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(3)记第(2)问所求的定点为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的一个动点,试根据
上的一个动点,试根据![]() 面积
面积![]() 的不同取值范围,讨论
的不同取值范围,讨论![]() 存在的个数,并说明理由.
存在的个数,并说明理由.
【答案】(1)![]() ;(2)过定点
;(2)过定点![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)由题意布列关于![]() 的方程组,从而得到椭圆方程;(2) 设直线
的方程组,从而得到椭圆方程;(2) 设直线![]() 方程:
方程: ![]() ,联立方程可得:
,联立方程可得: ![]() ,利用根与系数的关系及
,利用根与系数的关系及![]() ,得到
,得到![]() 过定点
过定点![]() .(3)设直线
.(3)设直线![]() 与椭圆
与椭圆![]() 相切,
相切, ![]() ,两切线到
,两切线到![]() 的距离分别为
的距离分别为![]() ,根据
,根据![]() 面积
面积![]() 的不同取值范围,讨论
的不同取值范围,讨论![]() 存在的个数.
存在的个数.
试题解析:
(1)由![]() 得:
得: ![]() ,所以
,所以![]() ………①
………①
又![]() 周长为
周长为![]() ,所以
,所以![]() ………②
………②
解①②方程组,得![]()
所以椭圆方程为![]()
(2)设直线![]() 方程:
方程: ![]() ,交点
,交点![]()
![]()
![]()
![]()
依题: ![]() 即:
即: ![]()
![]()
![]()
![]()
![]() 过定点
过定点![]() .
.
(3)![]() ,
, ![]()
设直线![]() 与椭圆
与椭圆![]() 相切,
相切,
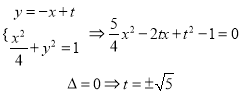
得两切线到![]() 的距离分别为
的距离分别为![]()
![]()
![]()
当![]() 时,
时, ![]() 个数为0个
个数为0个
当![]() 时,
时, ![]() 个数为1个
个数为1个
当![]() 时,
时, ![]() 个数为2个
个数为2个
当![]() 时,
时, ![]() 个数为3个
个数为3个
当![]() 时,
时, ![]() 个数为4个
个数为4个

【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪80元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成6元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其50天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 15 | 10 | 10 | 5 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 5 | 10 | 10 | 20 | 5 |
(1)现从甲公司记录的50天中随机抽取3天,求这3天送餐单数都不小于40的概率;
(2)若将频率视为概率,回答下列两个问题:
①记乙公司送餐员日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小王打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.