题目内容
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点。
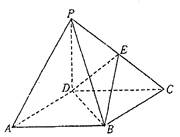
(1)证明PA平面BDE;
(2)求二面角B-DE-C的平面角的余弦值;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?
证明你的结论。

(1)证明PA平面BDE;
(2)求二面角B-DE-C的平面角的余弦值;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?
证明你的结论。
见解析
(1)以D为坐标原点,分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,设PD=CD=2,则A(2,0,0),P(0,0,2),E(0,1,1),B(2,2,0),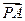 =(2,0,-2),
=(2,0,-2),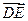 =(0,1,1),
=(0,1,1),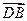 =(2,2,0)。
=(2,2,0)。
设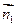 =(x,y,z)是平面BDE的一个法向量,
=(x,y,z)是平面BDE的一个法向量,
则由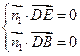 ,得
,得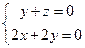 ;取x=-1,
;取x=-1,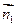 =(1,-1,1),
=(1,-1,1),
∵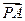 ·
·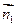 =2-2=0,∴
=2-2=0,∴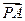 ⊥
⊥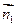 ,又PA?平面BDE,∴PA∥平面BDE。
,又PA?平面BDE,∴PA∥平面BDE。
(2) 由(1)知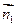 =(1,-1,1)是平面BDE的一个法向量,又
=(1,-1,1)是平面BDE的一个法向量,又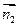 =
=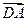 =(2,0,0)是平面DEC的一个法向量。
=(2,0,0)是平面DEC的一个法向量。
设二面角B-DE-C的平面角为θ,由图可知θ=<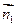 ,
,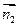 >,
>,
∴ cosθ=cos<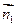 ,
,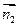 >=
>=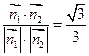 ,
,
故二面角B-DE-C余弦值为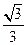 。
。
(3)∵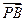 =(2,2,-2),
=(2,2,-2),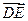 =(0,1,1),∴
=(0,1,1),∴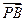 ·
·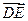 =0+2-2=0,∴PB⊥DE。
=0+2-2=0,∴PB⊥DE。
假设棱PB上存在点F,使PB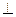 平面DEF,设
平面DEF,设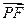 =λ
=λ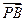 (0<λ<1),
(0<λ<1),
则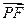 =(2λ, 2λ,-2λ),
=(2λ, 2λ,-2λ), =
=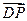 +
+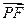 =(2λ, 2λ,2-2λ),
=(2λ, 2λ,2-2λ),
由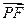 ·
· ="0" 得 4λ2 +4λ2-2λ(2-2λ)=0,
="0" 得 4λ2 +4λ2-2λ(2-2λ)=0,
∴ λ=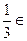 (0,1),此时PF=
(0,1),此时PF=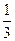 PB,
PB,
即在棱PB上存在点F,PF=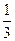 PB,使得PB⊥平面DEF。
PB,使得PB⊥平面DEF。
 =(2,0,-2),
=(2,0,-2),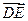 =(0,1,1),
=(0,1,1),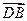 =(2,2,0)。
=(2,2,0)。设
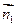 =(x,y,z)是平面BDE的一个法向量,
=(x,y,z)是平面BDE的一个法向量,则由
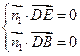 ,得
,得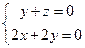 ;取x=-1,
;取x=-1,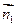 =(1,-1,1),
=(1,-1,1),∵
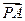 ·
·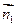 =2-2=0,∴
=2-2=0,∴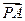 ⊥
⊥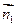 ,又PA?平面BDE,∴PA∥平面BDE。
,又PA?平面BDE,∴PA∥平面BDE。(2) 由(1)知
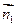 =(1,-1,1)是平面BDE的一个法向量,又
=(1,-1,1)是平面BDE的一个法向量,又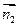 =
=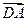 =(2,0,0)是平面DEC的一个法向量。
=(2,0,0)是平面DEC的一个法向量。设二面角B-DE-C的平面角为θ,由图可知θ=<
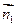 ,
,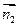 >,
>,∴ cosθ=cos<
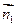 ,
,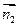 >=
>=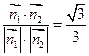 ,
,故二面角B-DE-C余弦值为
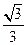 。
。(3)∵
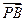 =(2,2,-2),
=(2,2,-2),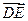 =(0,1,1),∴
=(0,1,1),∴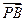 ·
·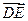 =0+2-2=0,∴PB⊥DE。
=0+2-2=0,∴PB⊥DE。假设棱PB上存在点F,使PB
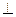 平面DEF,设
平面DEF,设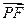 =λ
=λ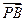 (0<λ<1),
(0<λ<1),则
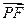 =(2λ, 2λ,-2λ),
=(2λ, 2λ,-2λ), =
=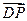 +
+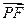 =(2λ, 2λ,2-2λ),
=(2λ, 2λ,2-2λ),由
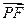 ·
· ="0" 得 4λ2 +4λ2-2λ(2-2λ)=0,
="0" 得 4λ2 +4λ2-2λ(2-2λ)=0,∴ λ=
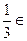 (0,1),此时PF=
(0,1),此时PF=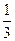 PB,
PB, 即在棱PB上存在点F,PF=
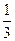 PB,使得PB⊥平面DEF。
PB,使得PB⊥平面DEF。
练习册系列答案
相关题目


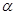 、
、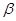 表示两个不同的平面,
表示两个不同的平面, 、
、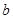 表示两条不同的直线,则下列命题正确的是( )
表示两条不同的直线,则下列命题正确的是( )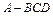 中,三条棱
中,三条棱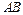 、
、 、
、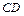 两两垂直,且
两两垂直,且 与平面
与平面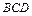 成
成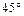 角,与平面
角,与平面 成
成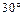 角.
角.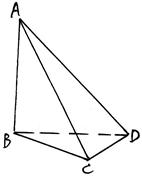
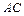 与平面
与平面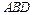 所成角的大小;
所成角的大小;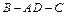 大小的余弦值.
大小的余弦值.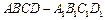 中,E、F、G分别为
中,E、F、G分别为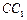 、
、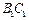 、
、 的中点,O为
的中点,O为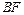 与
与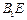 的交点,
的交点,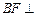 面
面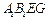
 与平面
与平面 中.
中.
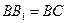 ,
,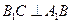 ,证明:平面
,证明:平面 平面
平面 ;
; 是
是 的中点,
的中点,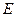 是
是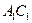 上的一点,
上的一点,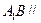 平面
平面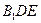 ,求
,求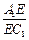 的值.
的值.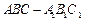 ,
,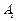 在底面ABC上的射影恰为AC的中点D,
在底面ABC上的射影恰为AC的中点D,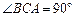 ,
, ,又知
,又知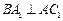
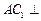 平面
平面
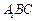 ;
;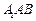 的距离;
的距离;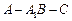 余弦值的大小.
余弦值的大小.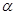 ,那么对于空间内的任意一条直线
,那么对于空间内的任意一条直线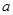 ,在平面
,在平面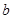 ,使得
,使得