题目内容
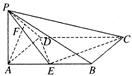
(本题满分12分)如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.SD=2,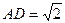 ,E是SD上的点。
,E是SD上的点。
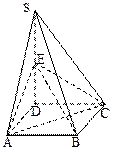
(Ⅰ)求证: AC⊥BE;
AC⊥BE;
(Ⅱ)求二面角C—AS—D的余弦值。
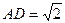 ,E是SD上的点。
,E是SD上的点。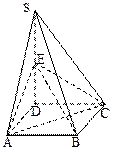
(Ⅰ)求证:
 AC⊥BE;
AC⊥BE;(Ⅱ)求二面角C—AS—D的余弦值。
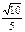
解:(Ⅰ)如图以D为原点建立空间直角坐标系
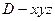 .则D(0,0,0),A(
.则D(0,0,0),A(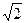 ,0,0),B(
,0,0),B(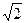 ,
,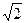 ,0),C(0,
,0),C(0,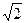 ,0),E(0,0,
,0),E(0,0,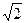 ),S(0,0,2),
),S(0,0,2),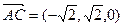 ,
,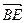 =
=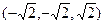 ……3分
……3分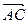 ·
·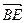 =2-2+0=0,所以
=2-2+0=0,所以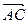 ⊥
⊥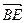 .即AC⊥BE.……………7分
.即AC⊥BE.……………7分(Ⅱ)由(Ⅰ)得
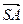 =(
=(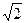 ,0,-2),
,0,-2),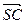 =(0,
=(0,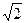 ,-2).
,-2).设平面ACS的法向量为
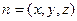 ,
,则由n⊥
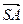 ,n⊥
,n⊥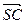 得
得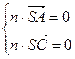 即
即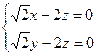
取
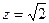 ,得.
,得. 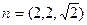 ……………………………11分
……………………………11分易知平面ASD的一个法向量为
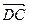 =(0
=(0 ,
,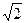 ,0).
,0).设二面角C—AS—D的平面角为θ.则
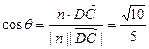 .
.即二面角C—AS—D的余弦值为
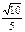 . ………………………………………12分
. ………………………………………12分
练习册系列答案
相关题目
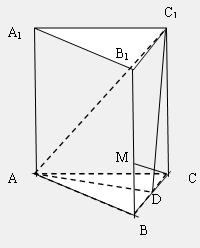
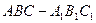 中,底面边长是2,D是BC的中点,M在BB1上,且
中,底面边长是2,D是BC的中点,M在BB1上,且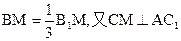 .
.
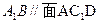 ;
; 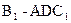 的体积;
的体积;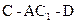 的余弦值.
的余弦值.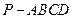 的底面是边长为2的正方形,
的底面是边长为2的正方形,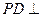
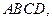
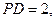
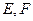 分别为
分别为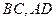 的中点,
的中点,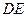 与面
与面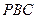 所成角的正弦值;
所成角的正弦值;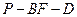 的正切值.
的正切值. 为两条直线,
为两条直线, 为两个平面,下列四个命题中真命题是 ( )
为两个平面,下列四个命题中真命题是 ( ) 所成角相等,则
所成角相等,则



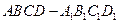 内接于球
内接于球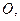
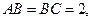
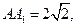 则
则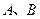 两点之间的球面距离
两点之间的球面距离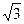 的正三棱柱形容器(下有底),可放置最大球的半径是
的正三棱柱形容器(下有底),可放置最大球的半径是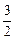
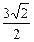
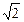
 ,
, 为不同直线,
为不同直线, ,
, 为不同平面,则下列选项:①
为不同平面,则下列选项:① ,
, ;②
;② ,
, ;③
;③ ;④
;④ ,其中能使
,其中能使 成立的充分条件有
成立的充分条件有