题目内容
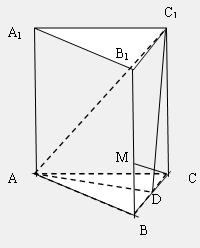
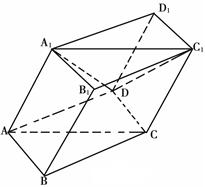
如图,在正三棱锥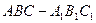 中,底面边长是2,D是BC的中点,M在BB1上,且
中,底面边长是2,D是BC的中点,M在BB1上,且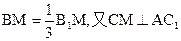 .
.
(1)求证: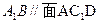 ;
;
(2)求三棱锥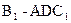 的体积;
的体积;
(3)求二面角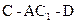 的余弦值.
的余弦值.
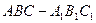 中,底面边长是2,D是BC的中点,M在BB1上,且
中,底面边长是2,D是BC的中点,M在BB1上,且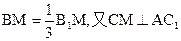 .
.
(1)求证:
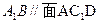 ;
; (2)求三棱锥
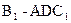 的体积;
的体积;(3)求二面角
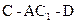 的余弦值.
的余弦值.(1)略;(2)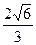 ;(3)
;(3)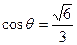
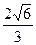 ;(3)
;(3)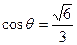
(1)证明:连接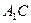 ,交
,交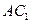 于点
于点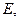 连接
连接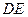 ,则
,则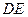 是
是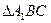 的中位线,
的中位线,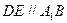 ,又
,又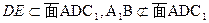 ,
,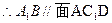 .
.
(2)在正三棱锥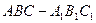 中,
中,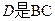 的中点,则
的中点,则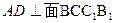 ,从而AD⊥MC,又CM⊥AC1,则CM和面ADC1内的两条相交直线AD,AC1都垂直,
,从而AD⊥MC,又CM⊥AC1,则CM和面ADC1内的两条相交直线AD,AC1都垂直,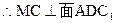 ,于是
,于是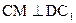 ,则
,则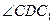 与
与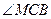 互余,则
互余,则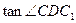 与
与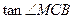 互为倒数,易得
互为倒数,易得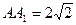 ,连B1D,
,连B1D,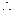
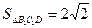 ,
,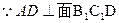 ,
, 三棱锥
三棱锥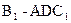 的体积为
的体积为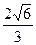 .
.
(3)过D作DH⊥AC,垂足为H,过H在面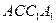 内作
内作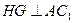 ,垂足为G,易证
,垂足为G,易证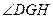 是二面角
是二面角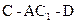 的平面角,在
的平面角,在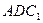 中,
中,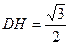 ,
,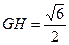 ,在
,在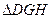 中,
中,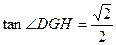
方法2:以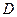 为坐标原点,
为坐标原点,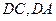 为
为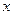
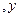 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设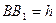 ,则
,则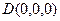 ,
,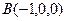 ,
,
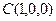 ,
,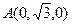 ,
,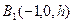 ,
,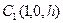 ,
, 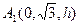 ,
,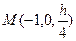 ,
,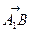
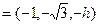 ,
,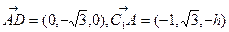 ,设平面
,设平面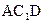 的法向量
的法向量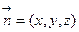 ,则
,则
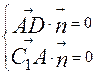

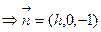 ,
,
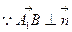
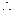
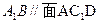 .
.
(2)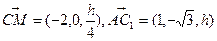 ,
,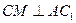 ,
,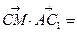
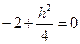 ,
,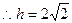 .平面
.平面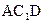 的法向量为
的法向量为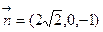 ,
,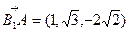 点
点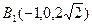 到平面
到平面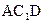 的距离
的距离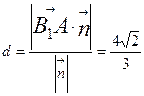 ,
,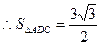 .
.
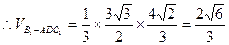 .
.
(3)由(2)知平面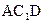 的法向量为
的法向量为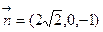 ,取
,取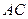 的中点为
的中点为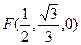 ,所以面
,所以面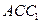 的法向量为
的法向量为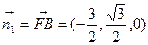 ,设二面角
,设二面角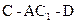 的平面角为
的平面角为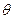 ,则
,则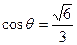 .
.
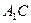 ,交
,交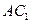 于点
于点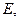 连接
连接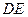 ,则
,则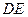 是
是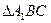 的中位线,
的中位线,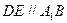 ,又
,又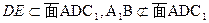 ,
,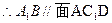 .
.(2)在正三棱锥
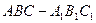 中,
中,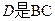 的中点,则
的中点,则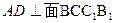 ,从而AD⊥MC,又CM⊥AC1,则CM和面ADC1内的两条相交直线AD,AC1都垂直,
,从而AD⊥MC,又CM⊥AC1,则CM和面ADC1内的两条相交直线AD,AC1都垂直,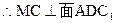 ,于是
,于是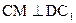 ,则
,则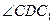 与
与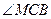 互余,则
互余,则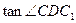 与
与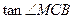 互为倒数,易得
互为倒数,易得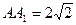 ,连B1D,
,连B1D,
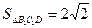 ,
,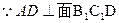 ,
, 三棱锥
三棱锥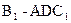 的体积为
的体积为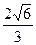 .
.(3)过D作DH⊥AC,垂足为H,过H在面
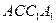 内作
内作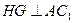 ,垂足为G,易证
,垂足为G,易证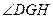 是二面角
是二面角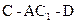 的平面角,在
的平面角,在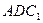 中,
中,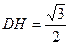 ,
,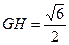 ,在
,在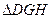 中,
中,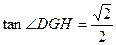
方法2:以
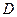 为坐标原点,
为坐标原点,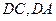 为
为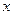
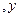 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设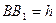 ,则
,则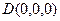 ,
,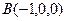 ,
,
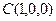 ,
,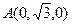 ,
,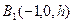 ,
,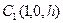 ,
, 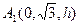 ,
,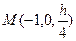 ,
,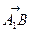
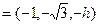 ,
,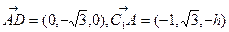 ,设平面
,设平面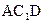 的法向量
的法向量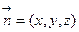 ,则
,则
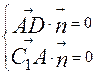

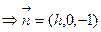 ,
,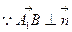
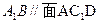 .
.(2)
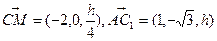 ,
,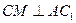 ,
,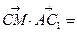
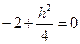 ,
,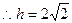 .平面
.平面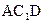 的法向量为
的法向量为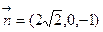 ,
,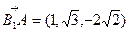 点
点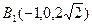 到平面
到平面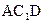 的距离
的距离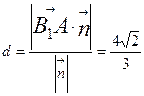 ,
,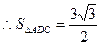 .
.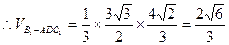 .
.(3)由(2)知平面
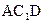 的法向量为
的法向量为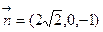 ,取
,取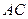 的中点为
的中点为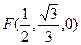 ,所以面
,所以面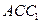 的法向量为
的法向量为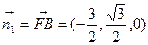 ,设二面角
,设二面角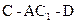 的平面角为
的平面角为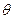 ,则
,则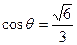 .
.
练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
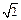 ,AA1=
,AA1=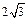 ,求AC1与平面ABC所成的角.
,求AC1与平面ABC所成的角.
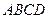 是边长为
是边长为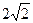 的正方形,
的正方形,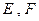 分别为
分别为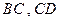 的中点,沿
的中点,沿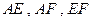 将
将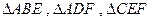 向同侧折叠且与平面
向同侧折叠且与平面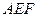 成直二面角,连接
成直二面角,连接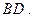
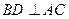 ;
;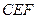 与平面
与平面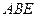 所成锐角的余弦值。
所成锐角的余弦值。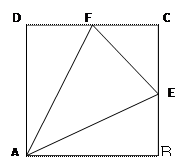

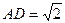 ,E是SD上的点。
,E是SD上的点。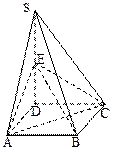
 AC⊥BE;
AC⊥BE; ,在
,在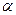 内有4个点,在
内有4个点,在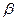 内有6个点,以这些点为顶点,最多可作 个三棱锥,在这些三棱锥中最多可以有 个不同的体积.
内有6个点,以这些点为顶点,最多可作 个三棱锥,在这些三棱锥中最多可以有 个不同的体积.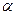 、
、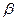 是两个不同平面,
是两个不同平面,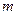 、
、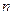 是两不同直线,下列命题中的假命题是 ( )
是两不同直线,下列命题中的假命题是 ( )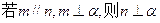
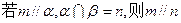
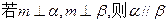
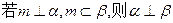
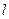 ⊥平面
⊥平面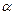 内所有直线”的充要条件是“
内所有直线”的充要条件是“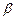 ”的必要不充分条件是“
”的必要不充分条件是“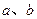 是异面直线,
是异面直线,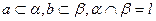 则
则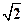 ,
,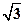 ,
,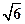 ,这个长方体对角线的长是( )
,这个长方体对角线的长是( )